题目内容
沿着圆柱的一条母线将圆柱剪开,可将侧面展到一个平面上,所得的矩形称为圆柱的侧面展开图,其中矩形长与宽分别是圆柱的底面圆周长和高(母线长),所以圆柱的侧面积S=2πrl,其中r为圆柱底面圆半径,l为母线长,现已知一个圆锥的底面半径为R,高为H,在其中有一个高为x的内接圆柱.
(1)求圆柱的侧面积;
(2)x为何值时,圆柱的侧面积最大?
(1)求圆柱的侧面积;
(2)x为何值时,圆柱的侧面积最大?
考点:基本不等式在最值问题中的应用,旋转体(圆柱、圆锥、圆台)
专题:综合题,不等式的解法及应用
分析:(1)根据相似三角形的性质,分析圆锥的高与底面半径的关系,可得圆柱的侧面积.
(2)由(1)中圆柱侧面积的表达式,结合二次函数的图象和性质,可得答案.
(2)由(1)中圆柱侧面积的表达式,结合二次函数的图象和性质,可得答案.
解答:
解:(1)设内接圆柱底面半径为r
由三角形相似得
=
,
所以r=
,
S圆柱侧=2π
•x=
(-x2+Hx)(0<x<H).
(2)S圆柱侧=
(-x2+Hx)=
•[-(x-
)2+
],又0<x<H,
所以当x=
时,S圆柱侧最大=
πRH.
由三角形相似得
| r |
| R |
| H-x |
| H |
所以r=
| (H-x)R |
| H |
S圆柱侧=2π
| (H-x)R |
| H |
| 2πR |
| H |
(2)S圆柱侧=
| 2πR |
| H |
| 2πR |
| H |
| H |
| 2 |
| H2 |
| 4 |
所以当x=
| H |
| 2 |
| 1 |
| 2 |
点评:本题考查圆柱的表面积,二次函数的图象和性质,熟练掌握二次函数的图象和性质是解答的关键.

练习册系列答案
相关题目
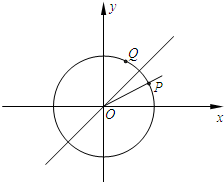 如图,已知单位圆上两点P,Q关于直线y=x对称,且以x轴正半轴为始边、以射线OP为终边的角的大小为x.
如图,已知单位圆上两点P,Q关于直线y=x对称,且以x轴正半轴为始边、以射线OP为终边的角的大小为x.