题目内容
已知点A（3，2），点P是抛物线y2=4x上的一个动点，求|PA|+|PF|的最小值及此时P点的坐标．
考点：抛物线的简单性质
专题：圆锥曲线的定义、性质与方程
分析：作PH垂直于准线，H为垂足，由抛物线的定义知，|PF|=|PH|，|PA|+|PF|=|PH|+|PA|，故当P、A、H三点共线时，|PH|+|PA|取得最小值，即|AH|．
解答：
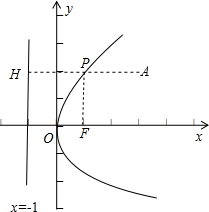解：记抛物线y2=4x的焦点为F（1，0），准线l是x=-1，
作PH垂直于准线，H为垂足，
由抛物线的定义知，|PF|=|PH|，|PA|+|PF|=|PH|+|PA|，
故当P、A、H三点共线时，|PH|+|PA|取得最小值为
|AH|=3-（-1）=4，
此时P（1，2）．
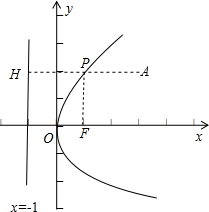解：记抛物线y2=4x的焦点为F（1，0），准线l是x=-1，作PH垂直于准线，H为垂足，
由抛物线的定义知，|PF|=|PH|，|PA|+|PF|=|PH|+|PA|，
故当P、A、H三点共线时，|PH|+|PA|取得最小值为
|AH|=3-（-1）=4，
此时P（1，2）．
点评：本题主要考查抛物线的定义、标准方程，以及简单性质的应用，属于中档题．
练习册系列答案
相关题目
已知等差数列{an}的前n项和为Sn，若
=a100
+a101
，且A、B、C三点共线（该直线不过点O），则S200等于（ ）
| OB |
| OA |
| OC |
| A、100 | B、101 |
| C、200 | D、201 |
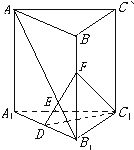如图，直三棱柱ABC-A1B1C1中，已知AC=BC=AA1=a，∠ACB=90°，D是A1B1中点．
在三棱柱ABC-A1B1C1中，侧面ABB1A1为矩形，AB=1，AA1=