题目内容
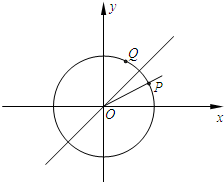 如图,已知单位圆上两点P,Q关于直线y=x对称,且以x轴正半轴为始边、以射线OP为终边的角的大小为x.
如图,已知单位圆上两点P,Q关于直线y=x对称,且以x轴正半轴为始边、以射线OP为终边的角的大小为x.(1)求点P,Q的坐标;
(2)若另有两点M(1,-1),N(-1,1),记f(x)=
| MP |
| NQ |
当点P在上半圆上运动(含与 x轴的交点)时,求函数f(x)的表达式;
(3)求函数f(x)最大值.
考点:两角和与差的正弦函数,平面向量数量积的运算,任意角的三角函数的定义
专题:三角函数的求值
分析:(1)由三角函数的定义可得点P,由对称性可得Q的坐标;(2)可得
和
的坐标,由数量积的运算可得f(x)的表达式;(3)由三角函数的知识,结合换元法和二次函数区间的最值可求.
| MP |
| NQ |
解答:
解:(1)由题意可得点P(cosx,sinx),
由对称性可得Q的坐标(sinx,cosx);
(2)又∵M(1,-1),N(-1,1),
∴
=(cosx-1,sinx+1),
=(sinx+1,cosx-1),
∴f(x)=
•
=2(cosx-1)(sinx+1),x∈[0,π];
(3)由(2)知函数f(x)=2(cosx-1)(sinx+1),x∈[0,π],
化简可得f(x)=2sinxcosx+2(cosx-sinx)-2,
令cosx-sinx=t,则t=cosx-sinx=
cos(x+
)∈[-1,
],
∴t2=1-2sinxcosx,代入上式可得y=1-t2+2t-2=-(t-1)2,
由二次函数的知识可知当t=
时,上式取最大值
∴函数f(x)最大值为:
由对称性可得Q的坐标(sinx,cosx);
(2)又∵M(1,-1),N(-1,1),
∴
| MP |
| NQ |
∴f(x)=
| MP |
| NQ |
(3)由(2)知函数f(x)=2(cosx-1)(sinx+1),x∈[0,π],
化简可得f(x)=2sinxcosx+2(cosx-sinx)-2,
令cosx-sinx=t,则t=cosx-sinx=
| 2 |
| π |
| 4 |
| ||
| 2 |
∴t2=1-2sinxcosx,代入上式可得y=1-t2+2t-2=-(t-1)2,
由二次函数的知识可知当t=
| ||
| 2 |
2
| ||
| 2 |
∴函数f(x)最大值为:
2
| ||
| 2 |
点评:本题考查两角和与差的三角函数公式,涉及向量的数量积和二次函数区间的最值,属中档题.

练习册系列答案
相关题目
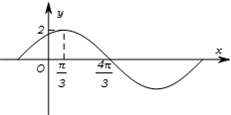 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<