题目内容
已知抛物线C1:x2=y,圆C2:x2+(y-4)2=1的圆心为点M.
(1)求点M到抛物线C1的准线的距离;
(2)已知点P是抛物线C1上一点(异于原点),过点P作圆C2的两条切线,交抛物线C1于A,B两点,若过M,P两点的直线l垂直于AB,求点P的坐标.
(1)求点M到抛物线C1的准线的距离;
(2)已知点P是抛物线C1上一点(异于原点),过点P作圆C2的两条切线,交抛物线C1于A,B两点,若过M,P两点的直线l垂直于AB,求点P的坐标.
考点:直线与圆锥曲线的综合问题
专题:综合题,圆锥曲线的定义、性质与方程
分析:(1)圆心M(0,4),抛物线C1的准线为y=-
,易求距离;
(2)设P(x0,x02),A(x1,x12),B(x2,x22),设过点P的圆C2的切线方程为y-x02=k(x-x0),即kx-y-kx0+x02=0①,则d=r=1⇒( x02-1)k2+2 x0(4-x02)k+( x02-4)2-1=0,设PA,PB的斜率为k1,k2(k1≠k2),则k1,k2是上述方程的两根,联立①与x2=y得x2-kx+kx0-x02=0,由韦达定理及kAB•KMP=-1可求得x0,进而得到点P坐标;
| 1 |
| 4 |
(2)设P(x0,x02),A(x1,x12),B(x2,x22),设过点P的圆C2的切线方程为y-x02=k(x-x0),即kx-y-kx0+x02=0①,则d=r=1⇒( x02-1)k2+2 x0(4-x02)k+( x02-4)2-1=0,设PA,PB的斜率为k1,k2(k1≠k2),则k1,k2是上述方程的两根,联立①与x2=y得x2-kx+kx0-x02=0,由韦达定理及kAB•KMP=-1可求得x0,进而得到点P坐标;
解答:
解:(1)圆心M(0,4),抛物线C1的准线为y=-
,
∴点M到抛物线C1的准线的距离为4-(-
)=
.
(2)设P(x0,x02),A(x1,x12),B(x2,x22),
则由题意得x0≠0,x0≠±1,x1≠x2,
设过点P的圆C2的切线方程为y-x02=k(x-x0),即kx-y-kx0+x02=0①,
则d=r=1⇒( x02-1)k2+2 x0(4-x02)k+( x02-4)2-1=0,
设PA,PB的斜率为k1,k2(k1≠k2),则k1,k2是上述方程的两根,
∴k1+k2=
,k1•k2=
,
将①代入x2=y得x2-kx+kx0-x02=0,
由于x0是此方程的根,点A或B是过点P作圆C2的两条切线与抛物线C1相交的交点,
故x0+x1=k1,x0+x2=k2,⇒x1=k1-x0,x2=k2-x0,
∴kAB=
=x1+x2=k1+k2-2x0=
-2x0,
又KMP=
,
∵MP⊥AB,∴kAB•KMP=[
-2x0]•(
)=-1,
⇒
•
=-1,解 x02=
,
∴点P的坐标为(±
,
).
| 1 |
| 4 |
∴点M到抛物线C1的准线的距离为4-(-
| 1 |
| 4 |
| 17 |
| 4 |
(2)设P(x0,x02),A(x1,x12),B(x2,x22),
则由题意得x0≠0,x0≠±1,x1≠x2,
设过点P的圆C2的切线方程为y-x02=k(x-x0),即kx-y-kx0+x02=0①,
则d=r=1⇒( x02-1)k2+2 x0(4-x02)k+( x02-4)2-1=0,
设PA,PB的斜率为k1,k2(k1≠k2),则k1,k2是上述方程的两根,
∴k1+k2=
| 2x0(x02-4) |
| x02-1 |
| (x02-4)2-1 |
| x02-1 |
将①代入x2=y得x2-kx+kx0-x02=0,
由于x0是此方程的根,点A或B是过点P作圆C2的两条切线与抛物线C1相交的交点,
故x0+x1=k1,x0+x2=k2,⇒x1=k1-x0,x2=k2-x0,
∴kAB=
| x12-x22 |
| x1-x2 |
| 2x0(x02-4) |
| x02-1 |
又KMP=
| x02-4 |
| x0 |
∵MP⊥AB,∴kAB•KMP=[
| 2x0(x02-4) |
| x02-1 |
| x02-4 |
| x0 |
⇒
| -6x0 |
| x02-1 |
| x02-4 |
| x0 |
| 23 |
| 5 |
∴点P的坐标为(±
| ||
| 5 |
| 23 |
| 5 |
点评:本题考查抛物线圆的方程,考查直线与圆锥曲线的位置关系,考查方程思想,考查学生综合运用知识分析解决问题的能力,综合性强,难度大.

练习册系列答案
 寒假学与练系列答案
寒假学与练系列答案
相关题目
 如图,在四棱柱ABCD-A1B1C1D1中,底面ABCD和侧面BCC1B1都是矩形,E是CD的中点,D1E⊥CD,AB=2BC=2.
如图,在四棱柱ABCD-A1B1C1D1中,底面ABCD和侧面BCC1B1都是矩形,E是CD的中点,D1E⊥CD,AB=2BC=2.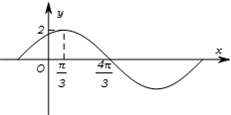 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ< 已知
已知