题目内容
已知a∈R,函数f(x)=ax2-(2+5a)x+5lnx.
(Ⅰ)若曲线y=f(x)在x=3和x=5处的切线互相平行,求a的值;
(Ⅱ)求f(x)的单调区间;
(Ⅲ)设g(x)=x2-
x,若对任意x1∈(0,
]均存在x2∈(0,
]使得f(x1)<g(x2),求a的取值范围.
(Ⅰ)若曲线y=f(x)在x=3和x=5处的切线互相平行,求a的值;
(Ⅱ)求f(x)的单调区间;
(Ⅲ)设g(x)=x2-
| 5 |
| 2 |
| 5 |
| 2 |
| 5 |
| 2 |
考点:导数在最大值、最小值问题中的应用
专题:导数的综合应用
分析:(Ⅰ)由f′(x)=2ax-(2+5a)+
,x>0和曲线y=f(x)在x=3和x=5处的切线互相平行,知f′(3)=f′(5),由此能求出a.
(Ⅱ)由f′(x)=2ax-(2+5a)+
=
,x>0,根据a的符号进行分类讨论,能够求出f(x)的单调递区间.
(Ⅲ)g(x)=x2-
x,对任意x1∈(0,
]均存在x2∈(0,
]使得f(x1)<g(x2),等价于在(0,
]上有f(x)max<g(x)max.由此能求出a的取值范围.
| 5 |
| x |
(Ⅱ)由f′(x)=2ax-(2+5a)+
| 5 |
| x |
| (ax-1)(2x-5) |
| x |
(Ⅲ)g(x)=x2-
| 5 |
| 2 |
| 5 |
| 2 |
| 5 |
| 2 |
| 5 |
| 2 |
解答:
解:(Ⅰ)∵f(x)=ax2-(2+5a)x+5lnx,
∴f′(x)=2ax-(2+5a)+
,x>0.
∵曲线y=f(x)在x=3和x=5处的切线互相平行,
∴f′(3)=f′(5),即6a-(2+5a)+
=10a-(2+5a)+1,
解得a=
.
(Ⅱ)∵f′(x)=2ax-(2+5a)+
=
,x>0,
①当a≤0时,x>0,ax-1<0,
在区间(0,
])上,f′(x)>0;在区间(
,+∞)上,f′(x)<0.
故f(x)的增区间是(0,
),减区间是(
,+∞).
②当0<a<
时,
>
,在区间(0,
)和(
,+∞)上,f′(x)>0;在区间(
,
)上,f′(x)<0.
故f(x)的增区间是(0,
),(
,+∞),减区间是(
,
).
③当a=
时,f′(x)=
,
故f(x)的单调递增区间是(0,+∞).
④当a>
时,0<
<
,在区间(0,
)和(
,+∞)上,f′(x)>0;在(
,
)上,f′(x)<0,
故f(x)的增区间是(0,
),(
,+∞),减区间是(
,
).
(Ⅲ)∵g(x)=x2-
x,对任意x1∈(0,
]均存在x2∈(0,
]使得f(x1)<g(x2),等价于在(0,
]上,有f(x)max<g(x)max.
g(x)=x2-
x在(0,
]的最大值g(x)max=g(
)=0.
由(Ⅱ)知:①当a≤
时,f(x)在(0,
]上单调递增,
故f(x)max=f(
)=
a-(2+5a)•
+5ln
=-
a-5+5ln
,
∴-
a-5+5ln
<0,解得a>
(ln
-1).
故
(ln
-1)<a≤
.
②当a>
时,f(x)在(0,
]上单调递增,在(
,
]上单调递减,
故f(x)max=f(
)=-5-
+5ln
=-
+5(ln
-1),
由a>
,知
<
<e,
∴ln
<ln
<1,∴ln
-1<0,
∴a>
.f(x)max<0.
综上所述a的取值范围是(
ln
-
,+∞).
∴f′(x)=2ax-(2+5a)+
| 5 |
| x |
∵曲线y=f(x)在x=3和x=5处的切线互相平行,
∴f′(3)=f′(5),即6a-(2+5a)+
| 5 |
| 3 |
解得a=
| 1 |
| 6 |
(Ⅱ)∵f′(x)=2ax-(2+5a)+
| 5 |
| x |
| (ax-1)(2x-5) |
| x |
①当a≤0时,x>0,ax-1<0,
在区间(0,
| 5 |
| 2 |
| 5 |
| 2 |
故f(x)的增区间是(0,
| 5 |
| 2 |
| 5 |
| 2 |
②当0<a<
| 2 |
| 5 |
| 1 |
| a |
| 5 |
| 2 |
| 5 |
| 2 |
| 1 |
| a |
| 5 |
| 2 |
| 1 |
| a |
故f(x)的增区间是(0,
| 5 |
| 2 |
| 1 |
| a |
| 5 |
| 2 |
| 1 |
| a |
③当a=
| 2 |
| 5 |
4(x-
| ||
| 5x |
故f(x)的单调递增区间是(0,+∞).
④当a>
| 2 |
| 5 |
| 1 |
| a |
| 5 |
| 2 |
| 1 |
| a |
| 5 |
| 2 |
| 1 |
| a |
| 5 |
| 2 |
故f(x)的增区间是(0,
| 1 |
| a |
| 5 |
| 2 |
| 1 |
| a |
| 5 |
| 2 |
(Ⅲ)∵g(x)=x2-
| 5 |
| 2 |
| 5 |
| 2 |
| 5 |
| 2 |
| 5 |
| 2 |
g(x)=x2-
| 5 |
| 2 |
| 5 |
| 2 |
| 5 |
| 2 |
由(Ⅱ)知:①当a≤
| 2 |
| 5 |
| 5 |
| 2 |
故f(x)max=f(
| 5 |
| 2 |
| 25 |
| 4 |
| 5 |
| 2 |
| 5 |
| 2 |
| 25 |
| 4 |
| 5 |
| 2 |
∴-
| 25 |
| 4 |
| 5 |
| 2 |
| 4 |
| 5 |
| 5 |
| 2 |
故
| 4 |
| 5 |
| 5 |
| 2 |
| 2 |
| 5 |
②当a>
| 2 |
| 5 |
| 1 |
| a |
| 1 |
| a |
| 5 |
| 2 |
故f(x)max=f(
| 1 |
| a |
| 1 |
| a |
| 1 |
| a |
| 1 |
| a |
| 1 |
| a |
由a>
| 2 |
| 5 |
| 1 |
| a |
| 5 |
| 2 |
∴ln
| 1 |
| a |
| 5 |
| 2 |
| 1 |
| a |
∴a>
| 2 |
| 5 |
综上所述a的取值范围是(
| 4 |
| 5 |
| 5 |
| 2 |
| 4 |
| 5 |
点评:本题考查导数的几何意义的应用,考查函数的单调区间的求法,考查满足条件的实数的取值范围的求法,综合性强,难度大.解题时要认真体会等价转化思想和分类讨论思想的合理运用.

练习册系列答案
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案
相关题目
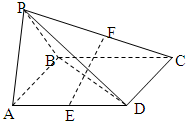 如图,四棱锥P-ABCD的底面是平行四边形,∠BAD=60°,平面PAB⊥平面ABCD,PA=PB=AB=
如图,四棱锥P-ABCD的底面是平行四边形,∠BAD=60°,平面PAB⊥平面ABCD,PA=PB=AB= 已知
已知