题目内容
已知圆台的上、下底面半径分别是2、5，且侧面面积等于两底面面积之和，求该圆台的母线长及体积大小．
考点：旋转体（圆柱、圆锥、圆台）
专题：空间位置关系与距离
分析：设圆台的母线长为l，求出圆台的上底面面积，圆台的下底面面积，利用圆台的底面面积等于圆台的侧面积求出圆台的母线，求出高，即可求解圆台的体积．
解答：
（本小题满分8分）
解：设圆台的母线长为l，则圆台的上底面面积为S上=π•22=4π，圆台的下底面面积为S下=π•52=25π，
所以圆台的底面面积为S=S上+S下=29π
又圆台的侧面积S侧=π（2+5）l=7πl，于是7πl=29π
即l=
为所求．
该圆台的高为
=
，于是该圆台的体积为V=
πh(S上+S下+
)=
．
解：设圆台的母线长为l，则圆台的上底面面积为S上=π•22=4π，圆台的下底面面积为S下=π•52=25π，
所以圆台的底面面积为S=S上+S下=29π
又圆台的侧面积S侧=π（2+5）l=7πl，于是7πl=29π
即l=
| 29 |
| 7 |
该圆台的高为
(
|
| 20 |
| 7 |
| 1 |
| 3 |
| S上S下 |
| 260π |
| 7 |
点评：本题考查圆台的表面积与体积的计算公式的应用，是基础题．
练习册系列答案
相关题目
已知sinα-cosα=-
，则tanα=（ ）
| 2 |
| A、-1 | ||||
| B、1 | ||||
C、-
| ||||
D、
|
已知等差数列{an}的前n项和为Sn，若
=a100
+a101
，且A、B、C三点共线（该直线不过点O），则S200等于（ ）
| OB |
| OA |
| OC |
| A、100 | B、101 |
| C、200 | D、201 |
如图，在四棱柱ABCD-A1B1C1D1中，底面ABCD和侧面BCC1B1都是矩形，E是CD的中点，D1E⊥CD，AB=2BC=2．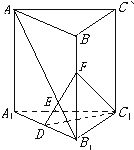
如图，直三棱柱ABC-A1B1C1中，已知AC=BC=AA1=a，∠ACB=90°，D是A1B1中点．