题目内容
设半径长为5的圆C满足条件:(1)截y轴所得弦长为6;(2)圆心在第一象限.并且到直线l:x+2y=0的距离为
.
(Ⅰ)求这个圆的方程;
(Ⅱ)求经过P(-1,0)与圆C相切的直线方程.
6
| ||
| 5 |
(Ⅰ)求这个圆的方程;
(Ⅱ)求经过P(-1,0)与圆C相切的直线方程.
考点:直线与圆的位置关系
专题:
分析:(Ⅰ)设圆心C(a,b),根据截y轴弦长为6,求出a,利用C到直线l:x+2y=0的距离为
,求出b,即可求这个圆的方程;
(Ⅱ)分类讨论,斜率存在时,设切线方程y=k(x+1),由C到直线y=k(x+1)的距离
=5,求出k,可得切线方程;斜率不存在时,方程x=-1,也满足题意.
6
| ||
| 5 |
(Ⅱ)分类讨论,斜率存在时,设切线方程y=k(x+1),由C到直线y=k(x+1)的距离
| |5k-1| | ||
|
解答:
解:(Ⅰ)由题设圆心C(a,b),半径r=5,
∵截y轴弦长为6,
∴a2+9=25,
∵a>0,
∴a=4…(2分)
由C到直线l:x+2y=0的距离为
,
∴d=
=
,
∵b>0,
∴b=1,
∴圆的方程为(x-4)2+(y-1)2=25;
(Ⅱ)①斜率存在时,设切线方程y=k(x+1),
由C到直线y=k(x+1)的距离
=5…(8分)
∴k=-
,
∴切线方程:12x+5y+12=0…(10分)
②斜率不存在时,方程x=-1,也满足题意,
由①②可知切线方程:12x+5y+12=0或x=-1…(12分).
∵截y轴弦长为6,
∴a2+9=25,
∵a>0,
∴a=4…(2分)
由C到直线l:x+2y=0的距离为
6
| ||
| 5 |
∴d=
| |4+2b| | ||
|
6
| ||
| 5 |
∵b>0,
∴b=1,
∴圆的方程为(x-4)2+(y-1)2=25;
(Ⅱ)①斜率存在时,设切线方程y=k(x+1),
由C到直线y=k(x+1)的距离
| |5k-1| | ||
|
∴k=-
| 12 |
| 5 |
∴切线方程:12x+5y+12=0…(10分)
②斜率不存在时,方程x=-1,也满足题意,
由①②可知切线方程:12x+5y+12=0或x=-1…(12分).
点评:本题考查圆的标准方程,考查直线与圆的位置关系,考查分类讨论的数学思想,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
一个正三角形的外接圆的半径为1,向该圆内随机投一点P,点P恰好落在正三角形内的概率是( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知定义在R上的函数f(x)满足f(2-x)为奇函数,函数f(x+3)关于直线x=1对称,则下列式子一定成立的是( )
| A、f(x-2)=f(x) |
| B、f(x-2)=f(x+6) |
| C、f(x-2)•f(x+2)=1 |
| D、f(-x)+f(x+1)=0 |
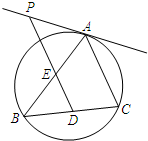 如图,△ABC内接于圆O,D为弦BC上一点,过D作直线DP∥AC,交AB于点E,交圆O
如图,△ABC内接于圆O,D为弦BC上一点,过D作直线DP∥AC,交AB于点E,交圆O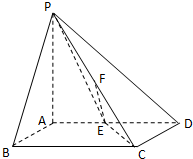 在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是正方形,且PA=AD=2,E,F分别是棱AD,PC的中点.
在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是正方形,且PA=AD=2,E,F分别是棱AD,PC的中点.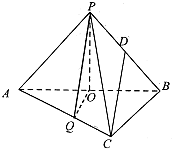 如图,三棱锥P-ABC中,已知平面PAB⊥平面ABC,AC⊥BC,AC=BC=2a,点O,D分别是AB,PB的中点,PO⊥AB,点Q在线段AC上,且AQ=2QC.
如图,三棱锥P-ABC中,已知平面PAB⊥平面ABC,AC⊥BC,AC=BC=2a,点O,D分别是AB,PB的中点,PO⊥AB,点Q在线段AC上,且AQ=2QC.