题目内容
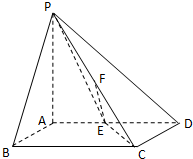 在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是正方形,且PA=AD=2,E,F分别是棱AD,PC的中点.
在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是正方形,且PA=AD=2,E,F分别是棱AD,PC的中点.(Ⅰ)求证:EF∥平面PAB;
(Ⅱ)求证:EF⊥平面PBC;
(Ⅲ)求二面角E-PC-D的大小.
考点:用空间向量求平面间的夹角,直线与平面平行的判定,直线与平面垂直的判定,与二面角有关的立体几何综合题
专题:空间位置关系与距离,空间角,空间向量及应用
分析:(Ⅰ)设G是PB的中点,连接AG,GF,由已知条件能推导出AEFG是平行四边形,从而能够证明EF∥平面PAB.
(Ⅱ)由已知条件推导出AG⊥PB,PA⊥BC,BC⊥AB,从而得到BC⊥AG,由此能够证明EF⊥平面PBC.
(Ⅲ) 以AB,AD,AP分别为x轴、y轴、z轴,建立空间直角坐标系A-xyz,利用向量法能求出二面角E-PC-D的大小.
(Ⅱ)由已知条件推导出AG⊥PB,PA⊥BC,BC⊥AB,从而得到BC⊥AG,由此能够证明EF⊥平面PBC.
(Ⅲ) 以AB,AD,AP分别为x轴、y轴、z轴,建立空间直角坐标系A-xyz,利用向量法能求出二面角E-PC-D的大小.
解答:
(本小题满分14分)
(Ⅰ)证明:设G是PB的中点,连接AG,GF
∵E,F分别是AD,PC的中点,∴GF
BC,AE
BC
∴GF
AE,∴AEFG是平行四边形,∴EF
AG…(2分)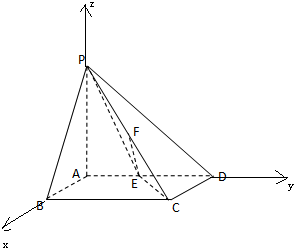
∵EF?平面PAB,AG?平面PAB,
∴EF∥平面PAB…(3分)
(Ⅱ)∵PA=AB,∴AG⊥PB,…(4分)
∵PA⊥ABCD,∴PA⊥BC,
又∵BC⊥AB,∴BC⊥平面PAB,
∴BC⊥AG,…(6分)
∵PB与BC相交,∴AG⊥平面PBC,
∵EF∥AG,∴EF⊥平面PBC.…(7分)
(Ⅲ) 以AB,AD,AP分别为x轴、y轴、z轴,
建立空间直角坐标系A-xyz,…(8分)
∵PA=AD=2,
∴E(0,1,0),C(2,2,0),P(0,0,2),F(1,1,1),
设H是PD的中点,连接AH,∵AG⊥平面PBC,
∴同理可证AH⊥平面PCD,∴
是平面PCD的法向量,
=(0,1,1)…(9分)
=(2,1,0),
=(0,-1,2)
设平面PEC的法向量
=(x,y,z),则
,
令y=2,则x=-1,z=1,∴
=(-1,2,1)…(12分)
∴cos<
,
>=
=
=
.…(13分)
∴二面角E-PC-D的大小为30°.…(14分)
(Ⅰ)证明:设G是PB的中点,连接AG,GF
∵E,F分别是AD,PC的中点,∴GF
| ||
. |
| 1 |
| 2 |
| ||
. |
| 1 |
| 2 |
∴GF
| ||
. |
| ||
. |

∵EF?平面PAB,AG?平面PAB,
∴EF∥平面PAB…(3分)
(Ⅱ)∵PA=AB,∴AG⊥PB,…(4分)
∵PA⊥ABCD,∴PA⊥BC,
又∵BC⊥AB,∴BC⊥平面PAB,
∴BC⊥AG,…(6分)
∵PB与BC相交,∴AG⊥平面PBC,
∵EF∥AG,∴EF⊥平面PBC.…(7分)
(Ⅲ) 以AB,AD,AP分别为x轴、y轴、z轴,
建立空间直角坐标系A-xyz,…(8分)
∵PA=AD=2,
∴E(0,1,0),C(2,2,0),P(0,0,2),F(1,1,1),
设H是PD的中点,连接AH,∵AG⊥平面PBC,
∴同理可证AH⊥平面PCD,∴
| AH |
| AH |
| EC |
| EP |
设平面PEC的法向量
| m |
|
令y=2,则x=-1,z=1,∴
| m |
∴cos<
| m |
| AH |
| ||||
|
|
| 3 | ||||
|
| ||
| 2 |
∴二面角E-PC-D的大小为30°.…(14分)
点评:本题考查直线与平面平行、直线与平面垂直的证明,考查二面角大小的求法,解题时要注意向量法的合理运用.

练习册系列答案
 天天练口算系列答案
天天练口算系列答案
相关题目
阅读如图的程序框图,运行相应的程序,则输出的结果是( )


| A、6 | B、5 | C、4 | D、3 |
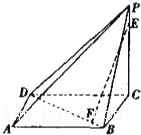 已知四棱锥P-ABCD中,PC⊥底面ABCD,PC=2,且底面ABCD是边长为1的正方形.E是最短的侧棱PC上的动点.
已知四棱锥P-ABCD中,PC⊥底面ABCD,PC=2,且底面ABCD是边长为1的正方形.E是最短的侧棱PC上的动点.