题目内容
 如图,△ABC内接于圆O,D为弦BC上一点,过D作直线DP∥AC,交AB于点E,交圆O
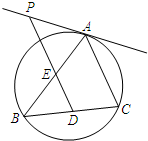
如图,△ABC内接于圆O,D为弦BC上一点,过D作直线DP∥AC,交AB于点E,交圆O在A点处的切线于点P.求证:△PAE∽△BDE.
考点:相似三角形的判定
专题:立体几何
分析:由题意,根据相似三角形的判定方法,找出两组对应角分别相等,即可证明△PAE∽△BDE.
解答:
证明:∵PA是圆O在点A处的切线,
∴∠PAB=∠C.
∵PD∥AC,
∴∠EDB=∠C,
∴∠PAE=∠PAB=∠C=∠BDE.
又∵∠PEA=∠BED,
∴△PAE∽△BDE.
∴∠PAB=∠C.
∵PD∥AC,
∴∠EDB=∠C,
∴∠PAE=∠PAB=∠C=∠BDE.
又∵∠PEA=∠BED,
∴△PAE∽△BDE.
点评:本题考查了相似三角形的判定问题,解题时应根据相似三角形的判定方法,找出两组对应角分别相等,即可证明.

练习册系列答案
相关题目
如图是计算
+
+
+…+
的值的一个程序框图,其中在判断框中应填入的条件是( )

| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 6 |
| 1 |
| 20 |

| A、i<10 | B、i>10 |
| C、i<20 | D、i>20 |
已知i是虚数单位,则
=( )
| 2-i |
| 1+2i |
| A、-i | ||||
B、
| ||||
| C、-1 | ||||
D、
|