题目内容
已知数列{an}中,a1=1,a2=2,an+1an-1=anan-1+an2(n∈N+,n≥2).
(Ⅰ)求证:{
}是等差数列;
(Ⅱ)设gn(x)=
,f(x)=g1(x)+g2(x)+g3(x)+…+gn(x),求f(x)的解析式;
(Ⅲ)求证:对?n∈N+,不等式f(2)<
gn(3)恒成立.
(Ⅰ)求证:{
| an+1 |
| an |
(Ⅱ)设gn(x)=
| anxn-1 |
| (n-1)! |
(Ⅲ)求证:对?n∈N+,不等式f(2)<
| 3 |
| n |
考点:数列与不等式的综合
专题:等差数列与等比数列
分析:(Ⅰ)由已知条件推导出
=
+1,由此能证明{
}是等差数列.
(Ⅱ)由(Ⅰ)知
=n+1,从而得到gn(x)=
=nxn-1,由此利用分类讨论思想和错位相减法能求出f(x)的解析式.
(Ⅲ)由已知条件推导出f(2)=
-
=(n-1)2n+1,
gn(3)=3n,由此利用数学归纳法能证明对?n∈N+,不等式f(2)<
gn(3)恒成立.
| an+1 |
| an |
| an |
| an-1 |
| an+1 |
| an |
(Ⅱ)由(Ⅰ)知
| an+1 |
| an |
| anxn-1 |
| (n-1)! |
(Ⅲ)由已知条件推导出f(2)=
| 1-2n |
| (1-2)2 |
| n2n |
| 1-2 |
| 3 |
| n |
| 3 |
| n |
解答:
(Ⅰ)证明:∵an+1an-1=anan-1+an2,
∴
=
+1,∴
-
=1,
∴{
}是公差是1的等差数列.…(4分)
(Ⅱ)解:∵a1=1,a2=2,{
}是公差是1的等差数列,
∴
=n+1,
∴an=
•
…
•a1=n•(n-1)…2•1=n!…(6分)
∴gn(x)=
=nxn-1,
∴当x=1时,f(x)=f(1)=1+2+3+…+n=
…(7分)
当x≠1时,f(x)=1+2x+3x2+…+nxn-1.①
xf(x)=x+2x2+3x3+…+(n-1)xn-1+nxn.②
①-②,得:(1-x)f(x)=1+x+x2+…+xn-1-nxn=
-nxn,
∴f(x)=
-
,…(9分)
综上所述:f(x)=
.…(10分)
(Ⅲ)∵x≠1,∴f(2)=
-
=(n-1)2n+1,
又∵
gn(3)=3n,
∴验证知当n=1,2,3时不等式成立…(11分)
假设n=k(k>3),不等式成立,即3k>(k-1)2k+1,
两边乘以3得:3k+1>3(k-1)2k+3=k•2k+1+1+3(k-1)2k-k•2k+1+2,
又∵3(k-1)2k-k•2k+1+2=2k(3k-3-2k)+2=(k-3)2k+2>0,
∴3k+1>k•2k+1+1+3(k-1)2k-k2k+1+2>k•2k+1+1,
即n=k+1时不等式成立.故不等式恒成立.…(13分)
∴
| an+1 |
| an |
| an |
| an-1 |
| an+1 |
| an |
| an |
| an-1 |
∴{
| an+1 |
| an |
(Ⅱ)解:∵a1=1,a2=2,{
| an+1 |
| an |
∴
| an+1 |
| an |
∴an=
| an |
| an-1 |
| an-1 |
| an-2 |
| a2 |
| a1 |
∴gn(x)=
| anxn-1 |
| (n-1)! |
∴当x=1时,f(x)=f(1)=1+2+3+…+n=
| n(n+1) |
| 2 |
当x≠1时,f(x)=1+2x+3x2+…+nxn-1.①
xf(x)=x+2x2+3x3+…+(n-1)xn-1+nxn.②
①-②,得:(1-x)f(x)=1+x+x2+…+xn-1-nxn=
| 1-xn |
| 1-x |
∴f(x)=
| 1-xn |
| (1-x)2 |
| nxn |
| 1-x |
综上所述:f(x)=
|
(Ⅲ)∵x≠1,∴f(2)=
| 1-2n |
| (1-2)2 |
| n2n |
| 1-2 |
又∵
| 3 |
| n |
∴验证知当n=1,2,3时不等式成立…(11分)
假设n=k(k>3),不等式成立,即3k>(k-1)2k+1,
两边乘以3得:3k+1>3(k-1)2k+3=k•2k+1+1+3(k-1)2k-k•2k+1+2,
又∵3(k-1)2k-k•2k+1+2=2k(3k-3-2k)+2=(k-3)2k+2>0,
∴3k+1>k•2k+1+1+3(k-1)2k-k2k+1+2>k•2k+1+1,
即n=k+1时不等式成立.故不等式恒成立.…(13分)
点评:本题考查等差数列的证明,考查函数解析式的求法,考查不等式的证明,解题时要认真审题,注意错位相减法和数学归纳法的合理运用.

练习册系列答案
相关题目
在空间中,设α,β表示平面,m,n表示直线.则下列命题正确的是( )
| A、若m∥n,n⊥α,则m⊥α |
| B、若α⊥β,m?α,则m⊥β |
| C、若m上有无数个点不在α内,则m∥α |
| D、若m∥α,那么m与α内的任何直线平行 |
已知两条直线m,n和平面α,且m在α内,n在α外,则“n∥α”是“m∥n”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
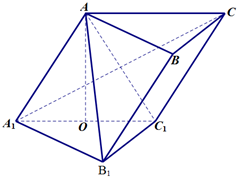 如图,在斜三棱柱ABC-A1B1C1中,点O是A1C1的中点,AO⊥平面A1B1C1.已知∠BCA=90°,AA1=AC=BC=2.
如图,在斜三棱柱ABC-A1B1C1中,点O是A1C1的中点,AO⊥平面A1B1C1.已知∠BCA=90°,AA1=AC=BC=2.