题目内容
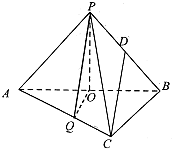 如图,三棱锥P-ABC中,已知平面PAB⊥平面ABC,AC⊥BC,AC=BC=2a,点O,D分别是AB,PB的中点,PO⊥AB,点Q在线段AC上,且AQ=2QC.
如图,三棱锥P-ABC中,已知平面PAB⊥平面ABC,AC⊥BC,AC=BC=2a,点O,D分别是AB,PB的中点,PO⊥AB,点Q在线段AC上,且AQ=2QC.(Ⅰ)证明:CD∥平面OPQ
(Ⅱ)若二面角A-PB-C的余弦值的大小为
| ||
| 5 |
考点:与二面角有关的立体几何综合题,直线与平面平行的判定
专题:综合题,空间位置关系与距离,空间角
分析:(Ⅰ)连接AD,交PO于M,连接OD,QM,则利用三角形中位线的性质,结合AQ=2QC,证明MQ∥CD,利用线面平行的判定定理证明CD∥平面OPQ
(Ⅱ)作OH⊥PB于H,连接CH,证明∠CHO是二面角A-PB-C的平面角,利用二面角A-PB-C的余弦值的大小为
,求出HB,在Rt△POB中,由射影定理可得OB2=BH•BP,即可求PA.
(Ⅱ)作OH⊥PB于H,连接CH,证明∠CHO是二面角A-PB-C的平面角,利用二面角A-PB-C的余弦值的大小为
| ||
| 5 |
解答:
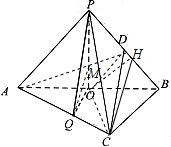 (Ⅰ)证明:连接AD,交PO于M,连接OD,QM,则
(Ⅰ)证明:连接AD,交PO于M,连接OD,QM,则
∵点O,D分别是AB,PB的中点,
∴OD∥AP,OD=
AP,
∴
=
=2=
,
∴MQ∥CD,
∵MQ?平面OPQ,CD?平面OPQ,
∴CD∥平面OPQ
(Ⅱ)解:连接OC,则
∵平面PAB⊥平面ABC,PO⊥AB,平面PAB∩平面ABC=AB,
∴PO⊥平面ABC,
∴PO⊥AB,PO⊥OC
∵AC=BC,点O是AB的中点,
∴OC⊥AB,且OA=OB=OC=
a,
作OH⊥PB于H,连接CH,则
∵PO⊥OC,OC⊥AB,PO∩AB=A,
∴OC⊥平面PAB,
∴CH⊥PB,
∴∠CHO是二面角A-PB-C的平面角,
∵二面角A-PB-C的余弦值的大小为
,
∴cos∠CHO=
,
∴tan∠CHO=2,
在Rt△COH中,∴HO=
a,
∴HB=
a,
在Rt△POB中,由射影定理可得OB2=BH•BP,
∴BP=
=
=
a
∴PA=
a.
 (Ⅰ)证明:连接AD,交PO于M,连接OD,QM,则
(Ⅰ)证明:连接AD,交PO于M,连接OD,QM,则∵点O,D分别是AB,PB的中点,
∴OD∥AP,OD=
| 1 |
| 2 |
∴
| AM |
| MD |
| AP |
| OD |
| AQ |
| QC |
∴MQ∥CD,
∵MQ?平面OPQ,CD?平面OPQ,
∴CD∥平面OPQ
(Ⅱ)解:连接OC,则
∵平面PAB⊥平面ABC,PO⊥AB,平面PAB∩平面ABC=AB,
∴PO⊥平面ABC,
∴PO⊥AB,PO⊥OC
∵AC=BC,点O是AB的中点,
∴OC⊥AB,且OA=OB=OC=
| 2 |
作OH⊥PB于H,连接CH,则
∵PO⊥OC,OC⊥AB,PO∩AB=A,
∴OC⊥平面PAB,
∴CH⊥PB,
∴∠CHO是二面角A-PB-C的平面角,
∵二面角A-PB-C的余弦值的大小为
| ||
| 5 |
∴cos∠CHO=
| ||
| 5 |
∴tan∠CHO=2,
在Rt△COH中,∴HO=
| ||
| 2 |
∴HB=
| ||
| 2 |
在Rt△POB中,由射影定理可得OB2=BH•BP,
∴BP=
| OB2 |
| BH |
| 2a2 | ||||
|
2
| ||
| 3 |
∴PA=
2
| ||
| 3 |
点评:本题考查线面平行,考查面面角,考查学生分析解决问题的能力,正确作出面面角,利用线面平行的判定定理是关键.

练习册系列答案
 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目
已知i是虚数单位,则
=( )
| 2-i |
| 1+2i |
| A、-i | ||||
B、
| ||||
| C、-1 | ||||
D、
|
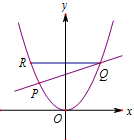 如图,设直线l:y=kx+
如图,设直线l:y=kx+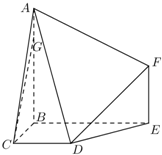 如图,多面体ABCDEF中,BA,BC,BE两两垂直,且AB∥EF,CD∥BE,AB=BE=2,BC=CD=EF=1.
如图,多面体ABCDEF中,BA,BC,BE两两垂直,且AB∥EF,CD∥BE,AB=BE=2,BC=CD=EF=1.