题目内容
已知定义在R上的函数f(x)满足f(2-x)为奇函数,函数f(x+3)关于直线x=1对称,则下列式子一定成立的是( )
| A、f(x-2)=f(x) |
| B、f(x-2)=f(x+6) |
| C、f(x-2)•f(x+2)=1 |
| D、f(-x)+f(x+1)=0 |
考点:抽象函数及其应用
专题:函数的性质及应用
分析:直接利用函数的奇偶性,以及函数的对称性,求出f(x-2)=f(x+6),得到结果即可.
解答:
解:令F(x)=f(2-x),∵f(2-x)为奇函数,
∴F(-x)=-F(x),即f(2+x)=-f(2-x),
∴即f(x)的图象关于点(2,0)对称,
令G(x)=f(x+3),G(x)图象关于直线x=1对称,
即G(1+x)=G(1-x),f[(1+x)+3]=f[(1-x)+3],f(4+x)=f(4-x),
即f(x)的图象关于直线x=4对称,
f(x)=f[4+(x-4)]=f[4-(x-4)]=f(8-x)
用x+6换表达式中的x,可得f(x-2)=f(x+6),
故选:B.
∴F(-x)=-F(x),即f(2+x)=-f(2-x),
∴即f(x)的图象关于点(2,0)对称,
令G(x)=f(x+3),G(x)图象关于直线x=1对称,
即G(1+x)=G(1-x),f[(1+x)+3]=f[(1-x)+3],f(4+x)=f(4-x),
即f(x)的图象关于直线x=4对称,
f(x)=f[4+(x-4)]=f[4-(x-4)]=f(8-x)
用x+6换表达式中的x,可得f(x-2)=f(x+6),
故选:B.
点评:本题考查抽象函数的应用,函数的奇偶性以及函数的对称性的应用,考查计算能力.

练习册系列答案
相关题目
已知两条直线m,n和平面α,且m在α内,n在α外,则“n∥α”是“m∥n”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
已知i是虚数单位,则
=( )
| 2-i |
| 1+2i |
| A、-i | ||||
B、
| ||||
| C、-1 | ||||
D、
|
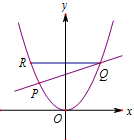 如图,设直线l:y=kx+
如图,设直线l:y=kx+