题目内容
如果二次函数f（x）=x2-mx+1存在零点，则m的取值范围是 ．
考点：二次函数的性质
专题：常规题型
分析：本题给出二次函数的解析式，要使函数有零点，要求对应的一元二次方程有实根，根的判别式非负，解得本题结论．
解答：
解：∵二次函数f（x）=x2-mx+1存在零点，
∴根的判别式△≥0，
即有：（-m）2-4≥0．
m≤-2或：m≥2．
故：m的取值范围是 （-∞，-2]∪[2，+∞）
∴根的判别式△≥0，
即有：（-m）2-4≥0．
m≤-2或：m≥2．
故：m的取值范围是 （-∞，-2]∪[2，+∞）
点评：本题考查的是二次函数问题，重点是二次函数零点的存在性，可以通过根的判别式去研究，也可以研究顶点纵坐标．
练习册系列答案
全优点练单元计划系列答案
相关题目
如图是计算
+
+
+…+
的值的一个程序框图，其中在判断框中应填入的条件是（ ）
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 6 |
| 1 |
| 20 |
| A、i＜10 | B、i＞10 |
| C、i＜20 | D、i＞20 |
已知i是虚数单位，则
=（ ）
| 2-i |
| 1+2i |
| A、-i | ||||
B、
| ||||
| C、-1 | ||||
D、
|
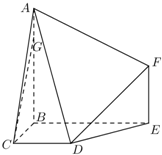如图，多面体ABCDEF中，BA，BC，BE两两垂直，且AB∥EF，CD∥BE，AB=BE=2，BC=CD=EF=1．