题目内容
11.我国古代数学著作《九章算术》有如下问题:“今有金箠,长五尺,斩本一尺,重四斤,斩末一尺,重二斤,问次一尺各重几何?”意思是:“现有一根金箠,长五尺,一头粗,一头细,在粗的一端截下1尺,重4斤;在细的一端截下1尺,重2斤;问依次每一尺各重多少斤?”根据上题的已知条件,若金箠由粗到细是均匀变化的,问第二尺与第四尺的重量之和为( )| A. | 6 斤 | B. | 9 斤 | C. | 9.5斤 | D. | 12 斤 |
分析 依题意,金箠由粗到细各尺构成一个等差数列,设首项a1=4,则a5=2,由此利用等差数列性质能求出结果.
解答 解:依题意,金箠由粗到细各尺构成一个等差数列,
设首项a1=4,则a5=2,
由等差数列性质得a2+a4=a1+a5=6,
所以第二尺与第四尺的重量之和为6斤.
故选:A.
点评 本题考查等差数列在生产生活中的实际应用,是基础题,解题时要认真审题,注意等差数列的性质的合理运用.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
1.某风险投资公司选择了三个投资项目,设每个项目成功的概率都为$\frac{1}{2}$,且相互之间设有影响,若每个项目成功都获利20万元,若每个项目失败都亏损5万元,该公司三个投资项目获利的期望为( )
| A. | 30万元 | B. | 22.5万元 | C. | 10万元 | D. | 7.5万元 |
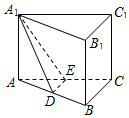 如图,在直三棱柱ABC-A1B1C1中,BC⊥AC,D,E分别是AB,AC的中点.
如图,在直三棱柱ABC-A1B1C1中,BC⊥AC,D,E分别是AB,AC的中点.