题目内容
2.若直线l1:x+ky+1=0(k∈R)与l2:(m+1)x-y+1=0(m∈R)相互平行,则这两直线之间距离的最大值为$\sqrt{2}$.分析 确定两条直线过定点,即可求出这两直线之间距离的最大值.
解答 解:由题意,直线l1:x+ky+1=0(k∈R)过定点(-1,0)
l2:(m+1)x-y+1=0(m∈R)过定点(0,1),
∴这两直线之间距离的最大值为$\sqrt{1+1}$=$\sqrt{2}$,
故答案为$\sqrt{2}$.
点评 本题考查这两直线之间距离的最大值,考查直线过定点,比较基础.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
10.某几何体的三视图如图所示,则该几何体的体积为( )


| A. | 6 | B. | $\frac{20}{3}$ | C. | 7 | D. | $\frac{22}{3}$ |
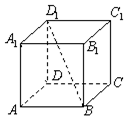 如图,在正方形ABCD-A1B1C1D1中,过对角线BD1的一个平面交AA1于E,交CC1于F,
如图,在正方形ABCD-A1B1C1D1中,过对角线BD1的一个平面交AA1于E,交CC1于F,