题目内容
6.若实数x,y,z满足x+2y+z=1,求x2+y2+z2的最小值.分析 利用条件x+2y+z=1,构造柯西不等式(x+y+z)2≤(x2+y2+z2)(12+22+12)进行解题即可.
解答 解:由柯西不等式,得(x+2y+z)2≤(12+22+12)•(x2+y2+z2),
即$x+2y+z≤\sqrt{{1^2}+{2^2}+{1^2}}•\sqrt{{x^2}+{y^2}+{z^2}}$,…(5分)
又因为x+2y+z=1,所以${x^2}+{y^2}+{z^2}≥\frac{1}{6}$,
当且仅当$\frac{x}{1}=\frac{y}{2}=\frac{z}{1}$,即$x=z=\frac{1}{6},y=\frac{1}{3}$时取等号.
综上,${({{x^2}+{y^2}+{z^2}})_{min}}=\frac{1}{6}$.…(10分)
点评 本题主要考查了函数的最值,以及柯西不等式的应用,解题的关键是利用(x+2y+z)2≤(x2+y2+z2)(12+22+12)进行解决.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
11.我国古代数学著作《九章算术》有如下问题:“今有金箠,长五尺,斩本一尺,重四斤,斩末一尺,重二斤,问次一尺各重几何?”意思是:“现有一根金箠,长五尺,一头粗,一头细,在粗的一端截下1尺,重4斤;在细的一端截下1尺,重2斤;问依次每一尺各重多少斤?”根据上题的已知条件,若金箠由粗到细是均匀变化的,问第二尺与第四尺的重量之和为( )
| A. | 6 斤 | B. | 9 斤 | C. | 9.5斤 | D. | 12 斤 |
15.如果直线l1:2x-y-1=0与直线l2:2x+(a+1)y+2=0平行,那么a等于( )
| A. | -2 | B. | -1 | C. | 1 | D. | 2 |
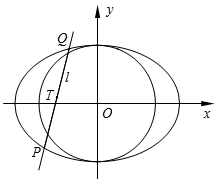 在平面直角坐标系xOy中,已知圆O:x2+y2=b2经过椭圆$E:\frac{x^2}{4}+\frac{y^2}{b^2}=1$(0<b<2)的焦点.
在平面直角坐标系xOy中,已知圆O:x2+y2=b2经过椭圆$E:\frac{x^2}{4}+\frac{y^2}{b^2}=1$(0<b<2)的焦点.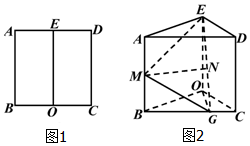 如图1,在边长为$2\sqrt{3}$的正方形ABCD中,E、O分别为 AD、BC的中点,沿 EO将矩形ABOE折起使得∠BOC=120°,如图2,点G 在BC上,BG=2GC,M、N分别为AB、EG中点.
如图1,在边长为$2\sqrt{3}$的正方形ABCD中,E、O分别为 AD、BC的中点,沿 EO将矩形ABOE折起使得∠BOC=120°,如图2,点G 在BC上,BG=2GC,M、N分别为AB、EG中点.