题目内容
3.已知函数f(x)=|2x-a|+|2x+3|,g(x)=|x-1|+2.(Ⅰ)若a=1,解不等式f(x)<6;
(Ⅱ)若对任意x1∈R,都有x2∈R,使得f(x1)=g(x2)成立,求实数a的取值范围.
分析 (Ⅰ)通过讨论x的范围,得到关于x的不等式组,解出即可;
(Ⅱ)问题转化为{y|y=f(x)}⊆{y|y=g(x)},分别求出f(x),g(x)的最小值,得到关于a的不等式,解出即可.
解答 解:(Ⅰ)当a=1时,f(x)<6,即|2x-1|+|2x+3|<6,
即$\left\{\begin{array}{l}x≤-\frac{3}{2}\\ 1-2x-2x-3<6\end{array}\right.$或$\left\{\begin{array}{l}-\frac{3}{2}<x<\frac{1}{2}\\ 2x+3+1-2x<6\end{array}\right.$或$\left\{\begin{array}{l}x≥\frac{1}{2}\\ 2x-1+2x+3<6.\end{array}\right.$,
∴$-2<x≤-\frac{3}{2}$或$-\frac{3}{2}<x<\frac{1}{2}$或$\frac{1}{2}≤x<1$,
∴-2<x<1,
所以不等式f(x)<6的解集为{x|-2<x<1}.
(Ⅱ)对任意x1∈R,都有x2∈R,使得f(x1)=g(x2)成立,
则有{y|y=f(x)}⊆{y|y=g(x)},
又f(x)=|2x-a|+|2x+3|≥|(2x-a)-(2x+3)|=|a+3|,
g(x)=|x-1|+2≥2,从而|a+3|≥2,
解得a≤-5或a≥-1,
故a∈(-∞,-5]∪[-1,+∞).
点评 本题考查了解绝对值不等式问题,考查分类讨论思想以及函数的最值问题,是一道中档题.

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案
相关题目
11.我国古代数学著作《九章算术》有如下问题:“今有金箠,长五尺,斩本一尺,重四斤,斩末一尺,重二斤,问次一尺各重几何?”意思是:“现有一根金箠,长五尺,一头粗,一头细,在粗的一端截下1尺,重4斤;在细的一端截下1尺,重2斤;问依次每一尺各重多少斤?”根据上题的已知条件,若金箠由粗到细是均匀变化的,问第二尺与第四尺的重量之和为( )
| A. | 6 斤 | B. | 9 斤 | C. | 9.5斤 | D. | 12 斤 |
8.已知向量$\vec a,\vec b$,那么$\frac{1}{2}(2\vec a-4\vec b)+2\vec b$等于( )
| A. | $\vec a-2\vec b$ | B. | $\overrightarrow{a}$-4$\vec b$ | C. | $\vec a$ | D. | $\vec b$ |
15.如果直线l1:2x-y-1=0与直线l2:2x+(a+1)y+2=0平行,那么a等于( )
| A. | -2 | B. | -1 | C. | 1 | D. | 2 |
13.已知集合A={x∈Z|x≥2},B={1,2,3},则A∩B=( )
| A. | ∅ | B. | {2} | C. | {2,3} | D. | {x|2≤x<3} |
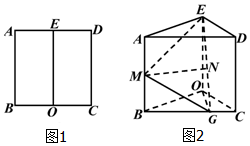 如图1,在边长为$2\sqrt{3}$的正方形ABCD中,E、O分别为 AD、BC的中点,沿 EO将矩形ABOE折起使得∠BOC=120°,如图2,点G 在BC上,BG=2GC,M、N分别为AB、EG中点.
如图1,在边长为$2\sqrt{3}$的正方形ABCD中,E、O分别为 AD、BC的中点,沿 EO将矩形ABOE折起使得∠BOC=120°,如图2,点G 在BC上,BG=2GC,M、N分别为AB、EG中点.