题目内容
设函数f(x)的定义域为D,如果?x∈D,?y∈D,使
=1成立,则称函数f(x)在定义域上为“相依函数”.给出下列五个函数①y=x3;②y=e-x;③y=lgx;④y=2cosx+1;⑤y=x+
,则早其定义域上为“相依函数”的函数序号是 .(填出所有满足条件的函数符号)
| f(x)+f(y) |
| 2 |
| 1 |
| x |
考点:命题的真假判断与应用,函数的值
专题:函数的性质及应用
分析:函数①y=x3,可直接取任意的x1∈R,验证求出唯一x2=
,即可得到成立.
y=4sinx,因为y=4sinx是R上的周期函数,不成立.
②y=e-x,特殊值法代入验证不成立成立.即可得到答案.
③y=lgx,定义域为x>0,值域为R且单调,显然成立.
④y=2cosx+1,函数是R上的周期函数,函数的值域[-1,3]判断正误即可.
⑤y=x+
,利用特例以及函数的值域判断即可.
| 3 | 2-x13 |
y=4sinx,因为y=4sinx是R上的周期函数,不成立.
②y=e-x,特殊值法代入验证不成立成立.即可得到答案.
③y=lgx,定义域为x>0,值域为R且单调,显然成立.
④y=2cosx+1,函数是R上的周期函数,函数的值域[-1,3]判断正误即可.
⑤y=x+
| 1 |
| x |
解答:
解:①y=x3,取任意的x1∈R,由
=1,解得x2=
,可以得到唯一的x2∈D.故满足条件.
②y=e-x定义域为R,值域为y>0.对于x1=-3,f(x1)=e3.要使
=1成立,则f(x2)=2-e3<0不成立.
③y=lgx,定义域为x>0,值域为R且单调,显然必存在唯一的x2∈D,使
=1成立.
④y=2cosx+1,函数的值域为[-1,2],函数是R上的周期函数,存在x2∈D,使
=1成立.故满足条件.
⑤y=x+
,对于x1=1,f(x1)=2.要使
=1成立,则f(x2)=0,∵f(x)∈(-∞,-2]∪[2,+∞),不成立.
故答案为:①③④
| f(x1)+f(x2) |
| 2 |
| 3 | 2-x13 |
②y=e-x定义域为R,值域为y>0.对于x1=-3,f(x1)=e3.要使
| f(x1)+f(x2) |
| 2 |
③y=lgx,定义域为x>0,值域为R且单调,显然必存在唯一的x2∈D,使
| f(x1)+f(x2) |
| 2 |
④y=2cosx+1,函数的值域为[-1,2],函数是R上的周期函数,存在x2∈D,使
| f(x1)+f(x2) |
| 2 |
⑤y=x+
| 1 |
| x |
| f(x1)+f(x2) |
| 2 |
故答案为:①③④
点评:本题主要考查新定义的应用,考查学生的推理和判断能力.综合性较强.

练习册系列答案
相关题目
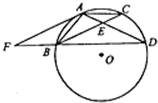 如图,点A,B,C,D在⊙O上,AB=AC,AD与BC相交于点E,AE=
如图,点A,B,C,D在⊙O上,AB=AC,AD与BC相交于点E,AE=