题目内容
15.已知函数f(x)为偶函数,当x<0时,f(x)=sinx+cosx,则f($\frac{π}{4}$)=( )| A. | 0 | B. | $\sqrt{2}$ | C. | -$\sqrt{2}$ | D. | 1 |
分析 由f(x)为偶函数便得到$f(\frac{π}{4})=f(-\frac{π}{4})$,这样代入x<0时的f(x)解析式便可求出$f(-\frac{π}{4})$,即得出$f(\frac{π}{4})$的值.
解答 解:根据条件,$f(\frac{π}{4})=f(-\frac{π}{4})=sin(-\frac{π}{4})+cos(-\frac{π}{4})$=$-\frac{\sqrt{2}}{2}+\frac{\sqrt{2}}{2}=0$.
故选:A.
点评 考查偶函数的定义,以及已知函数求值的方法,在已知函数求值时,注意自变量的取值范围.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
5.复数z1,z2在复平面内对应的点关于直线y=x对称,且z1=3+2i,则z1•z2=( )
| A. | 12+13i | B. | 13+12i | C. | -13i | D. | 13i |
6.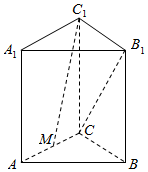 如图,在直三棱柱ABC-A1B1C1中,AB=BC=CC1=2,AC=2$\sqrt{3}$,M是AC的中点,则异面直线CB1与C1M所成角的余弦值为$\frac{\sqrt{14}}{28}$.
如图,在直三棱柱ABC-A1B1C1中,AB=BC=CC1=2,AC=2$\sqrt{3}$,M是AC的中点,则异面直线CB1与C1M所成角的余弦值为$\frac{\sqrt{14}}{28}$.
 如图,在直三棱柱ABC-A1B1C1中,AB=BC=CC1=2,AC=2$\sqrt{3}$,M是AC的中点,则异面直线CB1与C1M所成角的余弦值为$\frac{\sqrt{14}}{28}$.
如图,在直三棱柱ABC-A1B1C1中,AB=BC=CC1=2,AC=2$\sqrt{3}$,M是AC的中点,则异面直线CB1与C1M所成角的余弦值为$\frac{\sqrt{14}}{28}$.
3.已知复数z1=2+i,z2=3-2i,则z1•z2的虚部为( )
| A. | i | B. | -i | C. | 1 | D. | -1 |
10.已知正方体ABCD-A1B1C1D1,其棱长为2,P为该正方体内随机一点,则满足|PA|≤1的概率是( )
| A. | $\frac{π}{48}$ | B. | $\frac{π}{24}$ | C. | $\frac{π}{12}$ | D. | $\frac{1}{8}$ |
20.设集合A={x|-1<x≤2},B={x|0<x<2},则A∩B=( )
| A. | (-1,2] | B. | (0,2) | C. | (0,2] | D. | (1,+∞) |