题目内容
5.复数z1,z2在复平面内对应的点关于直线y=x对称,且z1=3+2i,则z1•z2=( )| A. | 12+13i | B. | 13+12i | C. | -13i | D. | 13i |
分析 求出复数的对称点的复数,利用复数的乘法运算法则求解即可.
解答 解:复数z1在复平面内关于直线y=x对称的点表示的复数z2=2+3i,
所以z1•z2=(3+2i)(2+3i)=13i.
故选:D.
点评 本题考查复数的乘法运算,以及复平面上的点与复数的关系,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
20.设x,y满足约束条件$\left\{\begin{array}{l}{y≥0}\\{x-y+1≥0}\\{x+y-3≤0}\end{array}\right.$,则z=2x-y的最小值为( )
| A. | -3 | B. | -2 | C. | -1 | D. | 2 |
17.已知集合U=R,函数$y=\sqrt{1-x}$的定义域为M,集合N={x|x2-x≤0},则下列结论正确的是( )
| A. | M∩N=N | B. | M∩(∁∪N)=∅ | C. | M∪N=U | D. | M⊆(∁∪N) |
14.已知直线a?平面α,直线b?平面β,α⊥β,则“a⊥b”是“a⊥β”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
15.已知函数f(x)为偶函数,当x<0时,f(x)=sinx+cosx,则f($\frac{π}{4}$)=( )
| A. | 0 | B. | $\sqrt{2}$ | C. | -$\sqrt{2}$ | D. | 1 |
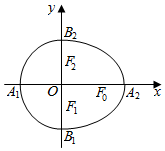 我们把由半椭圆$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1$(x≥0)与半椭圆$\frac{{y}^{2}}{{b}^{2}}+\frac{{x}^{2}}{{c}^{2}}=1$(x≤0)合成的曲线称作“果圆”,其中a2=b2+c2,a>0,b>c>0.如图,点F0,F1,F2是相应椭圆的焦点,A1,A2和B1,B2分别是“果圆”与x,y轴的交点.
我们把由半椭圆$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1$(x≥0)与半椭圆$\frac{{y}^{2}}{{b}^{2}}+\frac{{x}^{2}}{{c}^{2}}=1$(x≤0)合成的曲线称作“果圆”,其中a2=b2+c2,a>0,b>c>0.如图,点F0,F1,F2是相应椭圆的焦点,A1,A2和B1,B2分别是“果圆”与x,y轴的交点.