题目内容
7.在△ABC中,若AB=3,BC=5,CA=6,则$\overrightarrow{AB}•\overrightarrow{BC}$=1.分析 在△ABC中,由余弦定理和向量的数量积的运算即可求出结果
解答 解:由余弦定理可得AC2=AB2+BC2-2AB•BC•cosB,
∴36=9+25-2×3×5cosB,
∴cosB=-$\frac{1}{15}$,
∴$\overrightarrow{AB}•\overrightarrow{BC}$=|$\overrightarrow{AB}$|•|$\overrightarrow{BC}$|cos(π-B)=3×5×$\frac{1}{15}$=1,
故答案为:1.
点评 本题考查余弦定理,两个向量的数量积的定义,求出cosB的值,是解题的关键,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
17.已知集合U=R,函数$y=\sqrt{1-x}$的定义域为M,集合N={x|x2-x≤0},则下列结论正确的是( )
| A. | M∩N=N | B. | M∩(∁∪N)=∅ | C. | M∪N=U | D. | M⊆(∁∪N) |
15.已知函数f(x)为偶函数,当x<0时,f(x)=sinx+cosx,则f($\frac{π}{4}$)=( )
| A. | 0 | B. | $\sqrt{2}$ | C. | -$\sqrt{2}$ | D. | 1 |
2.要得到函数y=sin$\frac{1}{2}$x的图象,只要将函数y=cos2x的图象( )
| A. | 向右平移$\frac{π}{4}$个单位长度,再将各点的横坐标伸长为原来的4倍,纵坐标不变 | |
| B. | 向左平移$\frac{π}{4}$个单位长度,再将各点的横坐标缩短为原来的$\frac{1}{4}$倍,纵坐标不变 | |
| C. | 向左平移$\frac{π}{4}$个单位长度,再将各点的横坐标伸长为原来的4倍,纵坐标不变 | |
| D. | 向右平移$\frac{π}{4}$个单位长度,再将各点的横坐标缩短到原来的$\frac{1}{4}$,纵坐标不变 |
19.已知O在△ABC内,∠AOB=∠BOC=∠COA=120°,且AB⊥AC,AB=3,BC=5,则$\overrightarrow{OA}$•$\overrightarrow{OB}$+$\overrightarrow{OB}$•$\overrightarrow{OC}$+$\overrightarrow{OC}$•$\overrightarrow{OA}$的值为( )
| A. | 8 | B. | -$4\sqrt{3}$ | C. | 16 | D. | $16\sqrt{3}$ |
16.已知等差数列1,a,b,又4,a+2,b+1为等比数列,求该等差数列的公差( )
| A. | -1 | B. | 0 | C. | 2 | D. | 1 |
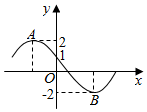 函数f(x)=2sin(ωx+φ)(ω>0,$\frac{π}{2}$≤φ≤π)的部分图象如图所示,其中A,B两点之间的距离为5,则ω=$\frac{π}{3}$.
函数f(x)=2sin(ωx+φ)(ω>0,$\frac{π}{2}$≤φ≤π)的部分图象如图所示,其中A,B两点之间的距离为5,则ω=$\frac{π}{3}$.