题目内容
4.在下列命题中,真命题的个数是( )①a∥α,b⊥α⇒a⊥b;②a∥α,b∥α⇒a∥b;
③a⊥α,b⊥α⇒a∥b;④a⊥b,b?α⇒a⊥α.
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
分析 根据线面的位置关系判断与性质定理,结合图形证明或举出反例.
解答 解:①由于a∥α,故而存在a′?α,使得a∥a′,又b⊥α,∴b⊥a′,∴a⊥b;故①正确.
②∵a∥α,b∥α,∴存在直线a′?α,b′?α,使得a∥a′,b∥b′,当a′,b′相交时,a,b相交或异面.故②错误.
③由线面垂直的性质定理“垂直于同一个平面的两条直线平行“可知③正确.
④由线面垂直的判定可知a垂直α内的一条直线b,不能保证a⊥α,故④错误.
故选:C.
点评 本题考查了空间直线与平面的位置关系,属于基础题.

练习册系列答案
相关题目
14.已知直线a?平面α,直线b?平面β,α⊥β,则“a⊥b”是“a⊥β”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
15.已知函数f(x)为偶函数,当x<0时,f(x)=sinx+cosx,则f($\frac{π}{4}$)=( )
| A. | 0 | B. | $\sqrt{2}$ | C. | -$\sqrt{2}$ | D. | 1 |
19.已知O在△ABC内,∠AOB=∠BOC=∠COA=120°,且AB⊥AC,AB=3,BC=5,则$\overrightarrow{OA}$•$\overrightarrow{OB}$+$\overrightarrow{OB}$•$\overrightarrow{OC}$+$\overrightarrow{OC}$•$\overrightarrow{OA}$的值为( )
| A. | 8 | B. | -$4\sqrt{3}$ | C. | 16 | D. | $16\sqrt{3}$ |
16.已知等差数列1,a,b,又4,a+2,b+1为等比数列,求该等差数列的公差( )
| A. | -1 | B. | 0 | C. | 2 | D. | 1 |
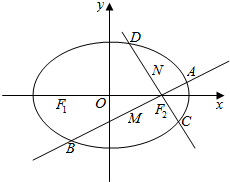 已知椭圆C:$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)的左、右焦点分别为F1,F2,且F1,F2与短轴的一个顶点Q构成一个等腰直角三角形,点P($\frac{\sqrt{2}}{2}$,$\frac{\sqrt{3}}{2}$)在椭圆C上.
已知椭圆C:$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)的左、右焦点分别为F1,F2,且F1,F2与短轴的一个顶点Q构成一个等腰直角三角形,点P($\frac{\sqrt{2}}{2}$,$\frac{\sqrt{3}}{2}$)在椭圆C上.