题目内容
10.已知正方体ABCD-A1B1C1D1,其棱长为2,P为该正方体内随机一点,则满足|PA|≤1的概率是( )| A. | $\frac{π}{48}$ | B. | $\frac{π}{24}$ | C. | $\frac{π}{12}$ | D. | $\frac{1}{8}$ |
分析 由题意可得概率为体积之比,分别求正方体的体积和八分之一球的体积可得.
解答 解:由题意可知总的基本事件为正方体内的点,可用其体积23=8度量,
满足|PA|≤1的基本事件为A为球心1为半径的求内部在正方体中的部分,
其体积为V=$\frac{1}{8}$×$\frac{4}{3}$π×13=$\frac{π}{6}$,故概率P=$\frac{\frac{π}{6}}{8}$=$\frac{π}{48}$.
故选:A.
点评 本题考查几何概型,涉及正方体和求的体积公式,属基础题.

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案
相关题目
20.设x,y满足约束条件$\left\{\begin{array}{l}{y≥0}\\{x-y+1≥0}\\{x+y-3≤0}\end{array}\right.$,则z=2x-y的最小值为( )
| A. | -3 | B. | -2 | C. | -1 | D. | 2 |
1.f(x)=x2+ax+b与坐标轴有三个交点A,B,C,且△ABC外心在y=x上,则a+b=( )
| A. | 1 | B. | -1 | C. | 0 | D. | -2 |
5.已知数列{an}满足an+1=2an,n∈N+,a3=4,则数列{an}的前5项和为( )
| A. | 32 | B. | 31 | C. | 64 | D. | 63 |
15.已知函数f(x)为偶函数,当x<0时,f(x)=sinx+cosx,则f($\frac{π}{4}$)=( )
| A. | 0 | B. | $\sqrt{2}$ | C. | -$\sqrt{2}$ | D. | 1 |
2.要得到函数y=sin$\frac{1}{2}$x的图象,只要将函数y=cos2x的图象( )
| A. | 向右平移$\frac{π}{4}$个单位长度,再将各点的横坐标伸长为原来的4倍,纵坐标不变 | |
| B. | 向左平移$\frac{π}{4}$个单位长度,再将各点的横坐标缩短为原来的$\frac{1}{4}$倍,纵坐标不变 | |
| C. | 向左平移$\frac{π}{4}$个单位长度,再将各点的横坐标伸长为原来的4倍,纵坐标不变 | |
| D. | 向右平移$\frac{π}{4}$个单位长度,再将各点的横坐标缩短到原来的$\frac{1}{4}$,纵坐标不变 |
19.已知O在△ABC内,∠AOB=∠BOC=∠COA=120°,且AB⊥AC,AB=3,BC=5,则$\overrightarrow{OA}$•$\overrightarrow{OB}$+$\overrightarrow{OB}$•$\overrightarrow{OC}$+$\overrightarrow{OC}$•$\overrightarrow{OA}$的值为( )
| A. | 8 | B. | -$4\sqrt{3}$ | C. | 16 | D. | $16\sqrt{3}$ |
20.函数y=2+sinx+cosx的最大值是( )
| A. | 2-$\sqrt{2}$ | B. | 2$+\sqrt{2}$ | C. | 2 | D. | 3 |
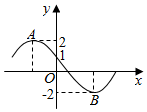 函数f(x)=2sin(ωx+φ)(ω>0,$\frac{π}{2}$≤φ≤π)的部分图象如图所示,其中A,B两点之间的距离为5,则ω=$\frac{π}{3}$.
函数f(x)=2sin(ωx+φ)(ω>0,$\frac{π}{2}$≤φ≤π)的部分图象如图所示,其中A,B两点之间的距离为5,则ω=$\frac{π}{3}$.