题目内容
5.在△ABC中,角A、B、C所对的边分别为a、b、c,已知2c-a=$\frac{bcosA}{cosB}$,且△ABC的面积为4$\sqrt{3}$,则b的最小值为4.分析 由正弦定理,三角形内角和定理,两角和的正弦函数公式化简已知,整理可得:2sinCcosB=sin(A+B)=sinC,由sinC≠0,解得cosB=$\frac{1}{2}$,结合范围B∈(0,π),可得B=$\frac{π}{3}$,利用三角形面积公式可求ac=16,由余弦定理及基本不等式即可解得b的最小值.
解答 解:∵2c-a=$\frac{bcosA}{cosB}$,
∴由正弦定理可得:cosB(2sinC-sinA)=sinBcosA,整理可得:2sinCcosB=sin(A+B)=sinC,
∵C∈(0,π),sinC≠0,
∴解得:cosB=$\frac{1}{2}$,由B∈(0,π),可得B=$\frac{π}{3}$,
又∵△ABC的面积为4$\sqrt{3}$=$\frac{1}{2}$acsinB=$\frac{1}{2}×\frac{\sqrt{3}}{2}$×ac,解得:ac=16,
∴由余弦定理可得:b2=a2+c2-2accosB=a2+c2-ac≥2ac-ac=ac=16,(当且仅当a=c=4时成立),
∴解得:b≥4.
故答案为:4.
点评 本题主要考查了正弦定理,三角形内角和定理,两角和的正弦函数公式,三角形面积公式,余弦定理及基本不等式在解三角形中的应用,考查了转化思想的应用,属于中档题.

练习册系列答案
相关题目
15.已知函数f(x)为偶函数,当x<0时,f(x)=sinx+cosx,则f($\frac{π}{4}$)=( )
| A. | 0 | B. | $\sqrt{2}$ | C. | -$\sqrt{2}$ | D. | 1 |
16.已知等差数列1,a,b,又4,a+2,b+1为等比数列,求该等差数列的公差( )
| A. | -1 | B. | 0 | C. | 2 | D. | 1 |
20.函数y=2+sinx+cosx的最大值是( )
| A. | 2-$\sqrt{2}$ | B. | 2$+\sqrt{2}$ | C. | 2 | D. | 3 |
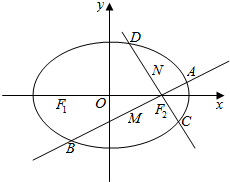 已知椭圆C:$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)的左、右焦点分别为F1,F2,且F1,F2与短轴的一个顶点Q构成一个等腰直角三角形,点P($\frac{\sqrt{2}}{2}$,$\frac{\sqrt{3}}{2}$)在椭圆C上.
已知椭圆C:$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)的左、右焦点分别为F1,F2,且F1,F2与短轴的一个顶点Q构成一个等腰直角三角形,点P($\frac{\sqrt{2}}{2}$,$\frac{\sqrt{3}}{2}$)在椭圆C上.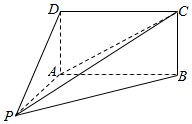 如图,四棱锥P-ABCD的底面ABCD为矩形,且PA=AD=1,AB=2,∠PAB=120°,∠PBC=90°.
如图,四棱锥P-ABCD的底面ABCD为矩形,且PA=AD=1,AB=2,∠PAB=120°,∠PBC=90°.