题目内容
6.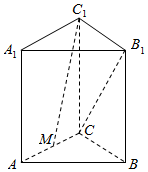 如图,在直三棱柱ABC-A1B1C1中,AB=BC=CC1=2,AC=2$\sqrt{3}$,M是AC的中点,则异面直线CB1与C1M所成角的余弦值为$\frac{\sqrt{14}}{28}$.
如图,在直三棱柱ABC-A1B1C1中,AB=BC=CC1=2,AC=2$\sqrt{3}$,M是AC的中点,则异面直线CB1与C1M所成角的余弦值为$\frac{\sqrt{14}}{28}$.
分析 以M为原点,MA为x轴,MB为y轴,过M作AC的垂线为z轴,建立空间直角坐标系,利用向量法能求出异面直线CB1与C1M所成角的余弦值.
解答 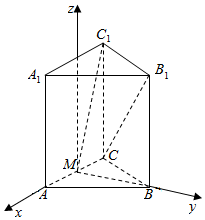 解:在直三棱柱ABC-A1B1C1中,AB=BC=CC1=2,AC=2$\sqrt{3}$,M是AC的中点,
解:在直三棱柱ABC-A1B1C1中,AB=BC=CC1=2,AC=2$\sqrt{3}$,M是AC的中点,
∴BM⊥AC,BM=$\sqrt{4-3}$=1,
以M为原点,MA为x轴,MB为y轴,过M作AC的垂线为z轴,建立空间直角坐标系,
C(-$\sqrt{3}$,0,0),B1(0,1,2),C1(-$\sqrt{3}$,0,2),M(0,0,0),
$\overrightarrow{C{B}_{1}}$=($\sqrt{3},1,2$),$\overrightarrow{M{C}_{1}}$=(-$\sqrt{3}$,0,2),
设异面直线CB1与C1M所成角为θ,
则cosθ=$\frac{|\overrightarrow{C{B}_{1}}•\overrightarrow{M{C}_{1}}|}{|\overrightarrow{C{B}_{1}}|•|\overrightarrow{M{C}_{1}}|}$=$\frac{1}{\sqrt{8}•\sqrt{7}}$=$\frac{\sqrt{14}}{28}$.
∴异面直线CB1与C1M所成角的余弦值为$\frac{\sqrt{14}}{28}$.
故答案为:$\frac{\sqrt{14}}{28}$.
点评 本题考查异面直线所成角的余弦值的求法,是中档题,解题时要认真审题,注意向量法的合理运用.

练习册系列答案
相关题目
17.已知集合U=R,函数$y=\sqrt{1-x}$的定义域为M,集合N={x|x2-x≤0},则下列结论正确的是( )
| A. | M∩N=N | B. | M∩(∁∪N)=∅ | C. | M∪N=U | D. | M⊆(∁∪N) |
14.已知直线a?平面α,直线b?平面β,α⊥β,则“a⊥b”是“a⊥β”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
1.f(x)=x2+ax+b与坐标轴有三个交点A,B,C,且△ABC外心在y=x上,则a+b=( )
| A. | 1 | B. | -1 | C. | 0 | D. | -2 |
15.已知函数f(x)为偶函数,当x<0时,f(x)=sinx+cosx,则f($\frac{π}{4}$)=( )
| A. | 0 | B. | $\sqrt{2}$ | C. | -$\sqrt{2}$ | D. | 1 |
16.已知等差数列1,a,b,又4,a+2,b+1为等比数列,求该等差数列的公差( )
| A. | -1 | B. | 0 | C. | 2 | D. | 1 |
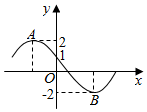 函数f(x)=2sin(ωx+φ)(ω>0,$\frac{π}{2}$≤φ≤π)的部分图象如图所示,其中A,B两点之间的距离为5,则ω=$\frac{π}{3}$.
函数f(x)=2sin(ωx+φ)(ω>0,$\frac{π}{2}$≤φ≤π)的部分图象如图所示,其中A,B两点之间的距离为5,则ω=$\frac{π}{3}$.