题目内容
已知x＞0，y＞0，证明（1+x+y2）（1+x2+y）≥9xy．
考点：不等式的证明
专题：证明题,不等式的解法及应用
分析：由均值不等式可得1+x+y2≥3
，1+x2+y≥3
，两式相乘可得结论．
| 3 | xy2 |
| 3 | x2y |
解答：
证明：由均值不等式可得1+x+y2≥3
，1+x2+y≥3
分别当且仅当x=y2=1，x2=y=1时等号成立，
∴两式相乘可得（1+x+y2）（1+x2+y）≥9xy．
| 3 | xy2 |
| 3 | x2y |
分别当且仅当x=y2=1，x2=y=1时等号成立，
∴两式相乘可得（1+x+y2）（1+x2+y）≥9xy．
点评：本题考查不等式的证明，正确运用均值不等式是关键．
练习册系列答案
学而优衔接教材南京大学出版社系列答案
小学课堂作业系列答案
金博士一点全通系列答案
相关题目
某几何体的三视图（单位：cm）如图所示，则该几何体的体积是（ ）
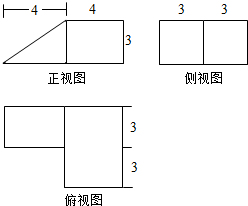
| A、72cm3 |
| B、90cm3 |
| C、108cm3 |
| D、138cm3 |
如图，在正方体ABCD-A1B1C1D1中，E、F、P、Q、M、N分别是棱AB、AD、DD1、BB1、A1B1、A1D1的中点，求证：