题目内容
 如图,在正方体ABCD-A1B1C1D1中,E、F、P、Q、M、N分别是棱AB、AD、DD1、BB1、A1B1、A1D1的中点,求证:
如图,在正方体ABCD-A1B1C1D1中,E、F、P、Q、M、N分别是棱AB、AD、DD1、BB1、A1B1、A1D1的中点,求证:(Ⅰ)直线BC1∥平面EFPQ;
(Ⅱ)直线AC1⊥平面PQMN.
考点:直线与平面垂直的判定,直线与平面平行的判定
专题:证明题,空间位置关系与距离
分析:(Ⅰ)要证直线BC1∥平面EFPQ,只需证BC1∥FP,且BC1?平面EFPQ即可,由AD1∥BC1,FP∥AD1即可证出;
(Ⅱ)要证直线AC1⊥平面PQMN,只需证出MN⊥AC1,且PN⊥AC1即可.
(Ⅱ)要证直线AC1⊥平面PQMN,只需证出MN⊥AC1,且PN⊥AC1即可.
解答:
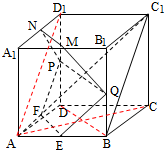 证明:(Ⅰ)在正方体ABCD-A1B1C1D1中,连接AD1,
证明:(Ⅰ)在正方体ABCD-A1B1C1D1中,连接AD1,
∵AD1∥BC1,且F、P分别是AD、DD1的中点,
∴FP∥AD1,∴BC1∥FP,
又FP?平面EFPQ,且BC1?平面EFPQ,
∴直线BC1∥平面EFPQ;
(Ⅱ)如图,
连接AC、BD,则AC⊥BD,∵CC1⊥平面ABCD,BD?平面ABCD,
∴CC1⊥BD;
又AC∩CC1=C,∴BD⊥平面ACC1,
又AC1?平面ACC1,∴BD⊥AC1;
又∵M、N分别是A1B1、A1D1的中点,
∴MN∥BD,∴MN⊥AC1;
同理可证PN⊥AC1,
又PN∩MN=N,∴直线AC1⊥平面PQMN.
 证明:(Ⅰ)在正方体ABCD-A1B1C1D1中,连接AD1,
证明:(Ⅰ)在正方体ABCD-A1B1C1D1中,连接AD1,∵AD1∥BC1,且F、P分别是AD、DD1的中点,
∴FP∥AD1,∴BC1∥FP,
又FP?平面EFPQ,且BC1?平面EFPQ,
∴直线BC1∥平面EFPQ;
(Ⅱ)如图,
连接AC、BD,则AC⊥BD,∵CC1⊥平面ABCD,BD?平面ABCD,
∴CC1⊥BD;
又AC∩CC1=C,∴BD⊥平面ACC1,
又AC1?平面ACC1,∴BD⊥AC1;
又∵M、N分别是A1B1、A1D1的中点,
∴MN∥BD,∴MN⊥AC1;
同理可证PN⊥AC1,
又PN∩MN=N,∴直线AC1⊥平面PQMN.
点评:本题考查了证明空间中的线面平行与线面垂直的问题,解题时应明确空间中的线面平行、线面垂直的判定方法是什么,也考查了逻辑思维能力与空间想象能力,是基础题.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
要制作一个容积为4m3,高为1m的无盖长方体容器,已知该容器的底面造价是每平方米20元,侧面造价是每平方米10元,则该容器的最低总造价是( )
| A、80元 | B、120元 |
| C、160元 | D、240元 |
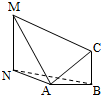 如图,为测量山高MN,选择A和另一座山的山顶C为测量观测点,从A点测得M点的仰角∠MAN=60°,C点的仰角∠CAB=45°,以及∠MAC=75°;从C点测得∠MCA=60°.已知山高BC=100m,则山高MN=
如图,为测量山高MN,选择A和另一座山的山顶C为测量观测点,从A点测得M点的仰角∠MAN=60°,C点的仰角∠CAB=45°,以及∠MAC=75°;从C点测得∠MCA=60°.已知山高BC=100m,则山高MN=