题目内容
直线l1:y=x+a和l2:y=x+b将单位圆C:x2+y2=1分成长度相等四段弧,则a2+b2= .
考点:直线与圆的位置关系,点到直线的距离公式
专题:直线与圆
分析:由题意可得,圆心(0,0)到两条直线的距离相等,且每段弧长都是圆周的
,即
=
=cos45°,由此求得a2+b2的值.
| 1 |
| 4 |
| |a| | ||
|
| |b| | ||
|
解答:
解:由题意可得,圆心(0,0)到两条直线的距离相等,且每段弧长都是圆周的
,
∴
=
=cos45°=
,∴a2+b2=2,
故答案为:2.
| 1 |
| 4 |
∴
| |a| | ||
|
| |b| | ||
|
| ||
| 2 |
故答案为:2.
点评:本题主要考查直线和圆的位置关系,点到直线的距离公式的应用,得到∴
=
=cos45°=
,是解题的关键,属于基础题.
| |a| | ||
|
| |b| | ||
|
| ||
| 2 |

练习册系列答案
相关题目
不等式组
的解集记为D,有下列四个命题:
p1:?(x,y)∈D,x+2y≥-2 p2:?(x,y)∈D,x+2y≥2
p3:?(x,y)∈D,x+2y≤3 p4:?(x,y)∈D,x+2y≤-1
其中真命题是( )
|
p1:?(x,y)∈D,x+2y≥-2 p2:?(x,y)∈D,x+2y≥2
p3:?(x,y)∈D,x+2y≤3 p4:?(x,y)∈D,x+2y≤-1
其中真命题是( )
| A、p2,p3 |
| B、p1,p4 |
| C、p1,p2 |
| D、p1,p3 |
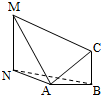 如图,为测量山高MN,选择A和另一座山的山顶C为测量观测点,从A点测得M点的仰角∠MAN=60°,C点的仰角∠CAB=45°,以及∠MAC=75°;从C点测得∠MCA=60°.已知山高BC=100m,则山高MN=
如图,为测量山高MN,选择A和另一座山的山顶C为测量观测点,从A点测得M点的仰角∠MAN=60°,C点的仰角∠CAB=45°,以及∠MAC=75°;从C点测得∠MCA=60°.已知山高BC=100m,则山高MN= 如图所示,函数y=f(x)的图象由两条射线和三条线段组成,若?x∈R,f(x)>f(x-1),则正实数a的取值范围为
如图所示,函数y=f(x)的图象由两条射线和三条线段组成,若?x∈R,f(x)>f(x-1),则正实数a的取值范围为 如图,P为⊙O外一点,过P点作⊙O的两条切线,切点分别为A,B,过PA的中点Q作割线交⊙O于C,D两点,若QC=1,CD=3,则PB=
如图,P为⊙O外一点,过P点作⊙O的两条切线,切点分别为A,B,过PA的中点Q作割线交⊙O于C,D两点,若QC=1,CD=3,则PB=