题目内容
设函数f(x)=1+(1+a)x-x2-x3,其中a>0.
(Ⅰ)讨论f(x)在其定义域上的单调性;
(Ⅱ)当x∈[0,1]时,求f(x)取得最大值和最小值时的x的值.
(Ⅰ)讨论f(x)在其定义域上的单调性;
(Ⅱ)当x∈[0,1]时,求f(x)取得最大值和最小值时的x的值.
考点:利用导数求闭区间上函数的最值,利用导数研究函数的单调性
专题:导数的综合应用
分析:(Ⅰ)利用导数判断函数的单调性即可;
(Ⅱ)利用(Ⅰ)的结论,讨论两根与1的大小关系,判断函数在[0,1]时的单调性,得出取最值时的x的取值.
(Ⅱ)利用(Ⅰ)的结论,讨论两根与1的大小关系,判断函数在[0,1]时的单调性,得出取最值时的x的取值.
解答:
解:(Ⅰ)f(x)的定义域为(-∞,+∞),f′(x)=1+a-2x-3x2,
由f′(x)=0,得x1=
,x2=
,x1<x2,
∴由f′(x)<0得x<
,x>
;
由f′(x)>0得
<x<
;
故f(x)在(-∞,
)和(
,+∞)单调递减,
在(
,
)上单调递增;
(Ⅱ)∵a>0,∴x1<0,x2>0,
①当a≥4时,x2≥1,由(Ⅰ)知,f(x)在[0,1]上单调递增,∴f(x)在x=0和x=1处分别取得最小值和最大值.
②当0<a<4时,x2<1,由(Ⅰ)知,f(x)在[0,x2]单调递增,在[x2,1]上单调递减,
因此f(x)在x=x2=
处取得最大值,又f(0)=1,f(1)=a,
∴当0<a<1时,f(x)在x=1处取得最小值;
当a=1时,f(x)在x=0和x=1处取得最小值;
当1<a<4时,f(x)在x=0处取得最小值.
由f′(x)=0,得x1=
-1-
| ||
| 3 |
-1+
| ||
| 3 |
∴由f′(x)<0得x<
-1-
| ||
| 3 |
-1+
| ||
| 3 |
由f′(x)>0得
-1-
| ||
| 3 |
-1+
| ||
| 3 |
故f(x)在(-∞,
-1-
| ||
| 3 |
-1+
| ||
| 3 |
在(
-1-
| ||
| 3 |
-1+
| ||
| 3 |
(Ⅱ)∵a>0,∴x1<0,x2>0,
①当a≥4时,x2≥1,由(Ⅰ)知,f(x)在[0,1]上单调递增,∴f(x)在x=0和x=1处分别取得最小值和最大值.
②当0<a<4时,x2<1,由(Ⅰ)知,f(x)在[0,x2]单调递增,在[x2,1]上单调递减,
因此f(x)在x=x2=
-1+
| ||
| 3 |
∴当0<a<1时,f(x)在x=1处取得最小值;
当a=1时,f(x)在x=0和x=1处取得最小值;
当1<a<4时,f(x)在x=0处取得最小值.
点评:本题主要考查利用导数研究函数的单调性及最值的知识,考查学生分类讨论思想的运用能力,属中档题.

练习册系列答案
 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
函数f(x)在x=x0处导数存在,若p:f′(x0)=0:q:x=x0是f(x)的极值点,则( )
| A、p是q的充分必要条件 |
| B、p是q的充分条件,但不是q的必要条件 |
| C、p是q的必要条件,但不是q的充分条件 |
| D、p既不是q的充分条件,也不是q的必要条件 |
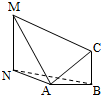 如图,为测量山高MN,选择A和另一座山的山顶C为测量观测点,从A点测得M点的仰角∠MAN=60°,C点的仰角∠CAB=45°,以及∠MAC=75°;从C点测得∠MCA=60°.已知山高BC=100m,则山高MN=
如图,为测量山高MN,选择A和另一座山的山顶C为测量观测点,从A点测得M点的仰角∠MAN=60°,C点的仰角∠CAB=45°,以及∠MAC=75°;从C点测得∠MCA=60°.已知山高BC=100m,则山高MN= 如图,P为⊙O外一点,过P点作⊙O的两条切线,切点分别为A,B,过PA的中点Q作割线交⊙O于C,D两点,若QC=1,CD=3,则PB=
如图,P为⊙O外一点,过P点作⊙O的两条切线,切点分别为A,B,过PA的中点Q作割线交⊙O于C,D两点,若QC=1,CD=3,则PB=