题目内容
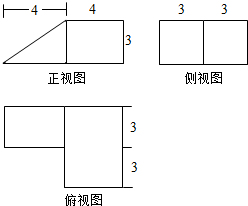
某几何体的三视图(单位:cm)如图所示,则该几何体的体积是( )

| A、72cm3 |
| B、90cm3 |
| C、108cm3 |
| D、138cm3 |
考点:由三视图求面积、体积
专题:立体几何
分析:利用三视图判断几何体的形状,利用三视图的数据求出几何体的体积即可.
解答:
解:由三视图可知:原几何体是由长方体与一个三棱柱组成,长方体的长宽高分别是:6,4,3;三棱柱的底面直角三角形的直角边长是4,3;高是3;
其几何体的体积为:V=3×4×6+
×3×4×3=90(cm3).
故选:B.
其几何体的体积为:V=3×4×6+
| 1 |
| 2 |
故选:B.
点评:本题考查三视图还原几何体,几何体的体积的求法,容易题.

练习册系列答案
相关题目
某公司10位员工的月工资(单位:元)为x1,x2,…,x10,其均值和方差分别为
和s2,若从下月起每位员工的月工资增加100元,则这10位员工下月工资的均值和方差分别为( )
. |
| x |
A、
| ||
B、
| ||
C、
| ||
D、
|
已知复数z=2-i,则z•
的值为( )
. |
| z |
| A、5 | ||
B、
| ||
| C、3 | ||
D、
|
下列函数中,满足“f(x+y)=f(x)f(y)”的单调递增函数是( )
| A、f(x)=x3 | ||
| B、f(x)=3x | ||
C、f(x)=x
| ||
D、f(x)=(
|
要制作一个容积为4m3,高为1m的无盖长方体容器,已知该容器的底面造价是每平方米20元,侧面造价是每平方米10元,则该容器的最低总造价是( )
| A、80元 | B、120元 |
| C、160元 | D、240元 |
函数f(x)在x=x0处导数存在,若p:f′(x0)=0:q:x=x0是f(x)的极值点,则( )
| A、p是q的充分必要条件 |
| B、p是q的充分条件,但不是q的必要条件 |
| C、p是q的必要条件,但不是q的充分条件 |
| D、p既不是q的充分条件,也不是q的必要条件 |