题目内容
设全集U是实数集R,M={x|y=log2(x2-4)},N={x|1<x<3} 则(∁RM)∩N=( )
| A、{x|-2≤x<1}| |
| B、{x|1<x≤2} |
| C、{x|-2≤x<2} |
| D、{x|x<2} |
考点:交、并、补集的混合运算
专题:集合
分析:求出M中x的范围确定出M,根据全集R求出M的补集,找出M补集与N的交集即可.
解答:
解:由M中y=log2(x2-4),得到x2-4>0,
解得:x>2或x<-2,即M={x|x<-2或x>2},
∵全集为R,
∴∁RM={x|-2≤x≤2},
∵N={x|1<x<3},
∴(∁RM)∩N={x|1<x≤2}.
故选:B.
解得:x>2或x<-2,即M={x|x<-2或x>2},
∵全集为R,
∴∁RM={x|-2≤x≤2},
∵N={x|1<x<3},
∴(∁RM)∩N={x|1<x≤2}.
故选:B.
点评:此题考查了交、并、补集的混合运算,熟练掌握各自的定义是解本题的关键.

练习册系列答案
相关题目
设a>0且a≠1若logax>1对x∈(0,
)恒成立,则a的取值范围是( )
| π |
| 4 |
A、(0,
| ||||
B、(0,
| ||||
C、(
| ||||
D、[
|
已知A={x|y=
+lnx},B={y|y=1-
},则A∩B=( )
| 1 |
| x-1 |
| x+2 |
| A、[0,1] |
| B、[0,1) |
| C、(0,1] |
| D、(0,1) |
有一段演绎推理:“因为对数函数y=logax是减函数;已知y=log2x是对数函数,所以y=log2x是减函数”,结论显然是错误的,这是因为( )
| A、推理形式错误 |
| B、小前提错误 |
| C、大前提错误 |
| D、非以上错误 |
不等式(x-3)(x-1)<0的解集是( )
| A、{x|1<x<3} |
| B、{x|x<1或x>3} |
| C、{x|x<1} |
| D、{x|x>3} |
下列选项中两个函数相同的是( )
A、y=x,y=
| ||||||
B、y=|x|,y=
| ||||||
| C、y=1,y=x0 | ||||||
D、y=
|
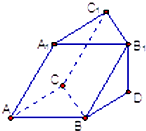 已知三棱柱ABC-A1B1C1的侧棱BB1在下底面的射影BD与AC平行,若BB1与底面所成角为30°,且∠B1BC=60°,则∠ACB的余弦值为( )
已知三棱柱ABC-A1B1C1的侧棱BB1在下底面的射影BD与AC平行,若BB1与底面所成角为30°,且∠B1BC=60°,则∠ACB的余弦值为( )