题目内容
下列选项中两个函数相同的是( )
A、y=x,y=
| ||||||
B、y=|x|,y=
| ||||||
| C、y=1,y=x0 | ||||||
D、y=
|
考点:判断两个函数是否为同一函数
专题:函数的性质及应用
分析:分别判断两个函数的定义域和对应法则是否一致,否则不是同一函数.
解答:
解:A.y=
的定义域为{x|x≠0},所以定义域不同,所以A不是同一函数.
B.两个函数的定义域相同,y=
=|x|,两个函数的对应法则相同,所以B是同一函数.
C.y=x0的定义域为{x|x≠0},所以定义域不同,所以C不是同一函数..
D.要使函数f(x)有意义,则
,即x≥2,要使函数g(x)有意义,则x2-4≥0,解得x≤-2或x≥2,所以两个函数的定义域不同,所以f(x),g(x)不能表示同一函数.
故选:B.
| x3 |
| x2 |
B.两个函数的定义域相同,y=
| x2 |
C.y=x0的定义域为{x|x≠0},所以定义域不同,所以C不是同一函数..
D.要使函数f(x)有意义,则
|
故选:B.
点评:本题主要考查判断两个函数是否为同一函数,判断的标准就是判断两个函数的定义域和对应法则是否一致,否则不是同一函数.

练习册系列答案
相关题目
设全集U是实数集R,M={x|y=log2(x2-4)},N={x|1<x<3} 则(∁RM)∩N=( )
| A、{x|-2≤x<1}| |
| B、{x|1<x≤2} |
| C、{x|-2≤x<2} |
| D、{x|x<2} |
已知变量x,y满足约束条件
,则y-2x的取值范围是( )
|
A、[-
| ||
B、[-
| ||
| C、[1,4] | ||
| D、[-1,1] |
双曲线
-
=1的焦点坐标为( )
| x2 |
| 16 |
| y2 |
| 9 |
A、(-
| ||||
B、(0,-
| ||||
| C、(-5,0)、(5,0) | ||||
| D、(0,-5)、(0,5) |
已知抛物线y2=2px(p>0)与双曲线
-
=1(a>0,b>0)有相同的焦点F,点A是两曲线的交点,且|AF|=p,则双曲线的离心率为( )
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
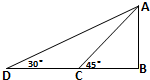 如图,D,C,B在地平面同一直线上,DC=10m,从D,C两地测得A点的仰角分别为30°和45°,则A点离地面的高AB等于( )
如图,D,C,B在地平面同一直线上,DC=10m,从D,C两地测得A点的仰角分别为30°和45°,则A点离地面的高AB等于( )| A、10m | ||
B、5
| ||
C、5(
| ||
D、5(
|
如图是一个空间几何体的三视图,则该几何体的表面积为( )


A、3+
| ||||
B、6+2
| ||||
C、3+2
| ||||
D、2+
|
f(sinx)=cos15x,则f(cosx)=( )
| A、sin15x |
| B、cos15x |
| C、-sin15x |
| D、-cos15x |
 如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AD=4,AB=2,以BD的中点O为球心、BD为直径的球面交PD于点M.
如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AD=4,AB=2,以BD的中点O为球心、BD为直径的球面交PD于点M.