题目内容
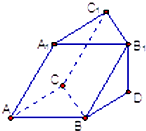 已知三棱柱ABC-A1B1C1的侧棱BB1在下底面的射影BD与AC平行,若BB1与底面所成角为30°,且∠B1BC=60°,则∠ACB的余弦值为( )
已知三棱柱ABC-A1B1C1的侧棱BB1在下底面的射影BD与AC平行,若BB1与底面所成角为30°,且∠B1BC=60°,则∠ACB的余弦值为( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点:三垂线定理
专题:计算题,空间位置关系与距离
分析:设B1在下底面上的射影为D,连接BD,过点D作DE垂直BC,交与点E,分别求出每条边长,在△BDE中利用余弦定理求出此角即可,再根据平行求出所求.
解答:
解:设B1在下底面上的射影为D,
连接BD,过点D作DE垂直BC,交与点E
∴∠B1BD是侧棱BB1与底面所成的角为30°
设B1B=2,则B1D=1,BD=
,
∵∠B1BC=60°∴BE=1,B1E=
,DE=
在△BDE中,cos∠DBE=
,
∵BD∥AC,∴∠DBE=∠ACB=
,
故选:C.
连接BD,过点D作DE垂直BC,交与点E
∴∠B1BD是侧棱BB1与底面所成的角为30°
设B1B=2,则B1D=1,BD=
| 3 |
∵∠B1BC=60°∴BE=1,B1E=
| 3 |
| 2 |
在△BDE中,cos∠DBE=
| ||
| 3 |
∵BD∥AC,∴∠DBE=∠ACB=
| ||
| 3 |
故选:C.
点评:本题主要考查了直线与平面所成的角,考查空间想象能力、运算能力和推理论证能力,属于基础题.

练习册系列答案
相关题目
已知集合M={x|(x-1)2<4,x∈R},N={-2.-1,0,1,2},则M∩N=( )
| A、{0,1,2} |
| B、{-1,0,1,2} |
| C、{-1,0,2,3} |
| D、{0,1,2,3} |
“x∈{3,a}”是不等式2x2-5x-3≥0成立的一个充分不必要条件,则实数a的取值范围是( )
| A、(3,+∞) | ||
B、(-∞,-
| ||
C、(-∞,-
| ||
D、(-∞,-
|
如果三个数2a,3,a-6成等差,则a的值为( )
| A、-1 | B、1 | C、3 | D、4 |
若函数y=f(x)为偶函数,且满足f(x+2)=-f(x),当x∈(0,1)时,f(x)=
+1,则f(
)=( )
| x |
| 2 |
| 7 |
| 2 |
| A、2 | ||
B、
| ||
C、
| ||
D、
|
设全集U是实数集R,M={x|y=log2(x2-4)},N={x|1<x<3} 则(∁RM)∩N=( )
| A、{x|-2≤x<1}| |
| B、{x|1<x≤2} |
| C、{x|-2≤x<2} |
| D、{x|x<2} |
如果x>0,y>0,且2x+y=2,则
+
的最小值是( )
| 2 |
| x |
| 2 |
| y |
| A、4 | ||
| B、3 | ||
C、2
| ||
D、3+2
|
双曲线
-
=1的焦点坐标为( )
| x2 |
| 16 |
| y2 |
| 9 |
A、(-
| ||||
B、(0,-
| ||||
| C、(-5,0)、(5,0) | ||||
| D、(0,-5)、(0,5) |