题目内容
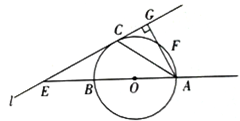 已知:直线AB过圆心O,交⊙O于A、B,直线AF交⊙O于A、F(不与B重合),直线l与⊙O相切于C,交AB于E,且与AF垂直,垂足为G,连接AC.
已知:直线AB过圆心O,交⊙O于A、B,直线AF交⊙O于A、F(不与B重合),直线l与⊙O相切于C,交AB于E,且与AF垂直,垂足为G,连接AC.(1)求证:∠BAC=∠CAG;
(2)求证:AC2=AE•AF.
考点:与圆有关的比例线段
专题:证明题,立体几何
分析:(1)连接BC,根据AB为⊙O的直径得到∠ECB与∠ACG互余,根据弦切角得到∠ECB=∠BAC,得到∠BAC与∠ACG互余,再根据∠CAG与∠ACG互余,得到∠BAC=∠CAG;
(2)连接CF,利用弦切角结合(1)的结论,可得∠GCF=∠ECB,再用外角进行等量代换,得到∠AFC=∠ACE,结合∠FAC=∠CAE得到△FAC∽△CAE,从而得到AC是AE、AF的比例中项,从而得到AC2=AE•AF.
(2)连接CF,利用弦切角结合(1)的结论,可得∠GCF=∠ECB,再用外角进行等量代换,得到∠AFC=∠ACE,结合∠FAC=∠CAE得到△FAC∽△CAE,从而得到AC是AE、AF的比例中项,从而得到AC2=AE•AF.
解答:
 证明:(1)连接BC,
证明:(1)连接BC,
∵AB为⊙O的直径…(2分)
∴∠ACB=90°⇒∠ECB+∠ACG=90°…(1分)
∵GC与⊙O相切于C,
∴∠ECB=∠BAC
∴∠BAC+∠ACG=90°…(4分)
又∵AG⊥CG⇒∠CAG+∠ACG=90°
∴∠BAC=∠CAG…(6分)
(2)由(1)可知∠EAC=∠CAF,连接CF
∵GE与⊙O相切于C,
∴∠GCF=∠CAF=∠BAC=∠ECB
∵∠AFC=∠GCF+90°,∠ACE=∠ECB+90°
∴∠AFC=∠ACE…(8分)
∵∠FAC=∠CAE
∴△FAC∽△CAE…(10分)
∴
=
∴AC2=AE•AF…(12分)
 证明:(1)连接BC,
证明:(1)连接BC,∵AB为⊙O的直径…(2分)
∴∠ACB=90°⇒∠ECB+∠ACG=90°…(1分)
∵GC与⊙O相切于C,
∴∠ECB=∠BAC
∴∠BAC+∠ACG=90°…(4分)
又∵AG⊥CG⇒∠CAG+∠ACG=90°
∴∠BAC=∠CAG…(6分)
(2)由(1)可知∠EAC=∠CAF,连接CF
∵GE与⊙O相切于C,
∴∠GCF=∠CAF=∠BAC=∠ECB
∵∠AFC=∠GCF+90°,∠ACE=∠ECB+90°
∴∠AFC=∠ACE…(8分)
∵∠FAC=∠CAE
∴△FAC∽△CAE…(10分)
∴
| AC |
| AE |
| AF |
| AC |
∴AC2=AE•AF…(12分)
点评:本题综合考查了弦切角、三角形的外角定理和相似三角形的性质等知识点,属于中档题.解题时要注意充分利用互余的角和弦切角进行等量代换,方可得到相似三角形.

练习册系列答案
 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目
曲线y=
与直线x=1,x=e2及x轴所围成的图形的面积是( )
| 1 |
| x |
| A、e2 |
| B、e2-1 |
| C、e |
| D、2 |
已知f(x)=log2x+2,x∈[1,4],则函数F(x)=[f(x)]2+f(x2)+3的最大值为( )
| A、13 | B、16 | C、25 | D、22 |
 如图,四棱锥P-ABCD的底面ABCD是平行四边形,BA=BD=
如图,四棱锥P-ABCD的底面ABCD是平行四边形,BA=BD=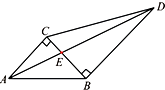 如图,两块直角三角板拼在一起,已知∠ABC=45°,∠BCD=60°.若记
如图,两块直角三角板拼在一起,已知∠ABC=45°,∠BCD=60°.若记 已知函数f(x)=ax2-|x|+2a-1(a为实常数).
已知函数f(x)=ax2-|x|+2a-1(a为实常数).