题目内容
函数f(x)=lnx+
-1的零点个数为( )
| 1 |
| x |
| A、0 | B、1 | C、2 | D、3 |
考点:函数零点的判定定理
专题:计算题,函数的性质及应用
分析:求出函数的导数,求出单调区间和极值、最值,判断符号,即可判断零点的个数.
解答:
解:函数f(x)=lnx+
-1(x>0),
导数f′(x)=
-
=
,
f′(x)>0得,x>1,为增区间;f′(x)<0,得,0<x<1,为减区间.
则x=1为极小值点,也为最小值点,
f(x)取最小值f(1)=0,
故零点个数为1.
故选B.
| 1 |
| x |
导数f′(x)=
| 1 |
| x |
| 1 |
| x2 |
| x-1 |
| x2 |
f′(x)>0得,x>1,为增区间;f′(x)<0,得,0<x<1,为减区间.
则x=1为极小值点,也为最小值点,
f(x)取最小值f(1)=0,
故零点个数为1.
故选B.
点评:本题考查函数的零点个数的求法,是基础题,解题时要认真审题,注意运用导数求最值,讨论最值符号的思想的合理运用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
若定义在区间[-2014,2014]上的函数,f(x)满足:对于任意的x1,x2∈[-2014,2014],都有f(x1+x2)=f(x1)+f(x2)-2012,且x>0时,有f(x)>2012,若f(x)的最大值、最小值分别为M,N,则M+N的值为( )
| A、4024 | B、2013 |
| C、2012 | D、4026 |
已知f(x)=log2x+2,x∈[1,4],则函数F(x)=[f(x)]2+f(x2)+3的最大值为( )
| A、13 | B、16 | C、25 | D、22 |
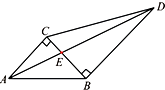 如图,两块直角三角板拼在一起,已知∠ABC=45°,∠BCD=60°.若记
如图,两块直角三角板拼在一起,已知∠ABC=45°,∠BCD=60°.若记 已知函数f(x)=ax2-|x|+2a-1(a为实常数).
已知函数f(x)=ax2-|x|+2a-1(a为实常数).