题目内容
已知F1、F2是椭圆C：
+
=1的两个焦点，P为椭圆C上的一点，如果△PF1F2是直角三角形，这样的点P有（ ）个．
| x2 |
| 8 |
| y2 |
| 4 |
| A、8 | B、6 | C、4 | D、2 |
考点：椭圆的简单性质
专题：计算题,圆锥曲线的定义、性质与方程
分析：求出椭圆的a，b，c，再讨论直角顶点的情况即有三种，分别考虑它们，即可得到答案．
解答：
解：椭圆C：
+
=1的a=2
，b=2，c=
=2，
由于△PF1F2是直角三角形，则若PF1⊥F1F2，则有两个，
若PF2⊥F1F2，则有两个，
若PF1⊥PF2，由于b=c，以F1F2为直径的圆与椭圆交于两点，
则有两个，
共有6个．
故选B．
| x2 |
| 8 |
| y2 |
| 4 |
| 2 |
| a2-b2 |
由于△PF1F2是直角三角形，则若PF1⊥F1F2，则有两个，
若PF2⊥F1F2，则有两个，
若PF1⊥PF2，由于b=c，以F1F2为直径的圆与椭圆交于两点，
则有两个，
共有6个．
故选B．
点评：本题考查椭圆的方程和性质，考查分类讨论的思想方法，考查运算能力，属于中档题和易错题．
练习册系列答案
优加精卷系列答案
相关题目
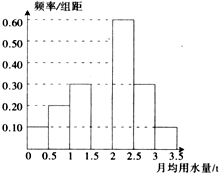我国是世界上严重缺水的国家之一，城市缺水问题较为突出．某市为了节约生活用水，计划在本市试行居民生活用水定额管理（即确定一个居民月均用水量标准?用水量不超过a的部分按照平价收费，超过a的部分按照议价收费）．为了较为合理地确定出这个标准，通过抽样获得了 100位居民某年的月均用水量（单位：t），制作了频率分布直方图，方程x2+y2+2x+2y-m=0，表示一个圆，则m的取值范围（ ）
| A、m≥-2 | B、m≤-2 |
| C、m＜-2 | D、m＞-2 |
已知A∈α，P∉α，
=（-
，
，
），平面α的一个法向量
=（0，-
，-
），则直线PA与平面α所成的角为（ ）
| PA |
| ||
| 2 |
| 1 |
| 2 |
| 2 |
| n |
| 1 |
| 2 |
| 2 |
| A、30° | B、45° |
| C、60° | D、150° |