题目内容
已知A∈α,P∉α,
=(-
,
,
),平面α的一个法向量
=(0,-
,-
),则直线PA与平面α所成的角为( )
| PA |
| ||
| 2 |
| 1 |
| 2 |
| 2 |
| n |
| 1 |
| 2 |
| 2 |
| A、30° | B、45° |
| C、60° | D、150° |
考点:用空间向量求直线与平面的夹角
专题:空间位置关系与距离
分析:设直线PA与平面α所成的角为θ.利用sinθ=|cos<
,
>|=
即可得出.
| PA |
| n |
|
| ||||
|
|
解答:
解:设直线PA与平面α所成的角为θ.
则sinθ=|cos<
,
>|=
=
=
.
∵θ∈[0°,90°].
∴θ=60°.
故选:C.
则sinθ=|cos<
| PA |
| n |
|
| ||||
|
|
| ||||||
|
| ||
| 2 |
∵θ∈[0°,90°].
∴θ=60°.
故选:C.
点评:本题考查了利用向量的夹角公式求线面角、数量积运算及其模的计算公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
函数y=esinx(-π≤x≤π)的大致图象为( )
A、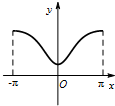 |
B、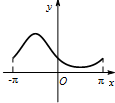 |
C、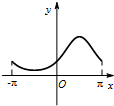 |
D、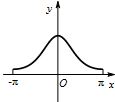 |
有50件产品,编号1-50,现在从中抽取5件检验,用系统抽样方法确定所抽的编号为( )
| A、5,10,15,20,25 |
| B、5,8,31,36,41 |
| C、5,15,25,35,45 |
| D、2,14,26,38,50 |
在正方体ABCD-A1B1C1D1中,若E是B1D1的中点,则直线BE垂直于( )
| A、AC |
| B、BD |
| C、A1D |
| D、A1D1 |
已知A(1,
),B(
-2,1),且
•
=0,sinβ≠0,sinα-kcosβ=0,则k=( )
| sinα |
| sin(α+2β) |
| sinα |
| sin(α-2β) |
| OA |
| OB |
A、
| ||||
B、-
| ||||
C、
| ||||
| D、以上都不对 |