题目内容
设全集U=R,函数f(x)=
+lg(a+3-x)的定义域为集合A,集合B={x|
≤2x≤32}.
(1)若a=-3,求A∩B;
(2)若A⊆∁UB,求实数a的取值范围.
| x-a |
| 1 |
| 4 |
(1)若a=-3,求A∩B;
(2)若A⊆∁UB,求实数a的取值范围.
考点:交、并、补集的混合运算
专题:函数的性质及应用,不等式的解法及应用,集合
分析:(1)把a=-3代入函数求值域A,化简集合B,然后根据交集的运算法则直接运算即可.
(2)求出函数的定义域,在求出B的补集,根据集合的包含关系即可.
(2)求出函数的定义域,在求出B的补集,根据集合的包含关系即可.
解答:
解:(1).B={x|
≤2x≤32}=[-2,5],∵a=-3,∴函数f(x)=
+lg(a+3-x)=
+lg(-x)定义域
为
,得-3≤x<0,集合A=[-3,0),∴A∩B=[-2,0).
(2).B=[-2,5],∁uB=(-∞,-2)∪(5,+∞),
又函数f(x)=
+lg(a+3-x)的定义域A={x|
}={x|a≤x<a+3},
要使A⊆∁UB,只要a>5或a+3<-2,∴a<-5,或a>5,
故a的取值范围是(-∞,-5)∪(5,+∞)
| 1 |
| 4 |
| x-a |
| x+3 |
为
|
(2).B=[-2,5],∁uB=(-∞,-2)∪(5,+∞),
又函数f(x)=
| x-a |
|
要使A⊆∁UB,只要a>5或a+3<-2,∴a<-5,或a>5,
故a的取值范围是(-∞,-5)∪(5,+∞)
点评:本题以集合运算为载体,考查了函数定义域,不等式的解法,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
有50件产品,编号1-50,现在从中抽取5件检验,用系统抽样方法确定所抽的编号为( )
| A、5,10,15,20,25 |
| B、5,8,31,36,41 |
| C、5,15,25,35,45 |
| D、2,14,26,38,50 |
在正方体ABCD-A1B1C1D1中,若E是B1D1的中点,则直线BE垂直于( )
| A、AC |
| B、BD |
| C、A1D |
| D、A1D1 |
已知函数f(x)=|x2-4x+3|,若方程[f(x)]2+bf(x)+c=0恰有七个不相同的实根,则实数b的取值范围是( )
| A、(-2,0) |
| B、(-2,-1) |
| C、(0,1) |
| D、(0,2) |
已知A(1,
),B(
-2,1),且
•
=0,sinβ≠0,sinα-kcosβ=0,则k=( )
| sinα |
| sin(α+2β) |
| sinα |
| sin(α-2β) |
| OA |
| OB |
A、
| ||||
B、-
| ||||
C、
| ||||
| D、以上都不对 |
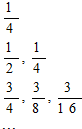 如图给出了一个“直角三角形数阵”:满足每一列成等差数列,从第三行起,每一行的数成等比数列,且每一行的公比相等,记第i行第j列的数为aij(i≥j,i,j∈N*),则a88=
如图给出了一个“直角三角形数阵”:满足每一列成等差数列,从第三行起,每一行的数成等比数列,且每一行的公比相等,记第i行第j列的数为aij(i≥j,i,j∈N*),则a88=