题目内容
设x>
,则当x= 时,x+
的最小值为 .
| 1 |
| 2 |
| 4 |
| 2x-1 |
考点:基本不等式在最值问题中的应用
专题:不等式的解法及应用
分析:直接利用基本不等式化简求解即可.
解答:
解:x>
,x+
=
+
+
≥2
+
,当且仅当x=
+
时取等号.
故答案为:
+
;2
+
.
| 1 |
| 2 |
| 4 |
| 2x-1 |
| 2x-1 |
| 2 |
| 4 |
| 2x-1 |
| 1 |
| 2 |
| 2 |
| 1 |
| 2 |
| 2 |
| 1 |
| 2 |
故答案为:
| 2 |
| 1 |
| 2 |
| 2 |
| 1 |
| 2 |
点评:本题考查基本不等式在最值中的应用,解题的关键是注意“一正、二定、三相等”的理解与应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
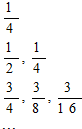 如图给出了一个“直角三角形数阵”:满足每一列成等差数列,从第三行起,每一行的数成等比数列,且每一行的公比相等,记第i行第j列的数为aij(i≥j,i,j∈N*),则a88=
如图给出了一个“直角三角形数阵”:满足每一列成等差数列,从第三行起,每一行的数成等比数列,且每一行的公比相等,记第i行第j列的数为aij(i≥j,i,j∈N*),则a88=