题目内容
4.在平面直角坐标系中,A(a,0),D(0,b),a≠0,C(0,-2),∠CAB=90°,D是AB的中点,当A在x轴上移动时,a与b满足的关系式为a2=2b;点B的轨迹E的方程为y=x2(x≠0).分析 求出AC和AB的斜率,根据∠CAB=90°得出斜率之间的关系,列方程即可得出答案.
解答 解:∵∠CAB=90°,∴kAC•kAB=-1,
又kAC=$\frac{2}{a}$,kAB=kAD=$\frac{b}{-a}$,
∴-$\frac{2b}{{a}^{2}}$=-1,即a2=2b.
设B(x,y),∵D是AB的中点,
∴x=-a,y=2b,
∵a2=2b,∴x2=y,
∴B点轨迹方程为y=x2(x≠0).
故答案为a2=2b,y=x2(x≠0).
点评 本题考查了轨迹方程的求解,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
14.下列说法错误的是( )
| A. | 回归直线过样本点的中心($\overline{x}$,$\overline{y}$) | |
| B. | 两个随机变量的线性相关性越强,则相关系数的绝对值就越接近于1 | |
| C. | 在回归直线方程$\stackrel{∧}{y}$=0.2x+0.8中,当解释变量x每增加1个单位时,预报变量$\stackrel{∧}{y}$平均增加0.2个单位 | |
| D. | 对分类变量X与Y,随机变量K2的观测值k越大,则判断“X与Y有关系”的把握程度越小 |
15.平面直角坐标系中,在由x轴、$x=\frac{π}{3}$、x=$\frac{5π}{3}$和y=2所围成的矩形中任取一点,满足不等关系y≤1-sin3x的概率是( )
| A. | $\frac{4π}{3}$ | B. | $\frac{π}{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{2}$ |
19.“函数f(x)=a+lnx(x≥e)存在零点”是“a<-1”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分不用必要条件 |
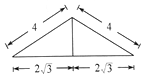
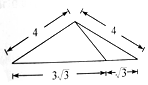
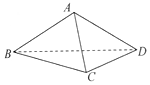 如图,在三棱锥A-BCD中,侧面ABD⊥底面BCD,BC⊥CD,AB=AD=4,BC=6,BD=4$\sqrt{3}$,该三棱锥三视图的正视图为( )
如图,在三棱锥A-BCD中,侧面ABD⊥底面BCD,BC⊥CD,AB=AD=4,BC=6,BD=4$\sqrt{3}$,该三棱锥三视图的正视图为( )

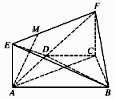 如图,在梯形ABCD中,AB∥CD,AD=CD=CB=a,∠ABC=60°,平面ACFE⊥平面ABCD,四边形ACFE是矩形,AE=a,点M在线段EF上,且MF=2EM.
如图,在梯形ABCD中,AB∥CD,AD=CD=CB=a,∠ABC=60°,平面ACFE⊥平面ABCD,四边形ACFE是矩形,AE=a,点M在线段EF上,且MF=2EM.