题目内容
12．
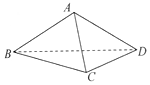如图，在三棱锥A-BCD中，侧面ABD⊥底面BCD，BC⊥CD，AB=AD=4，BC=6，BD=4$\sqrt{3}$，该三棱锥三视图的正视图为（ ）| A． |  | B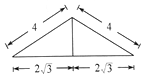． |  | C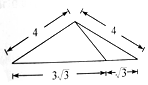． |  | D． |  |
分析 由题意，三棱锥三视图的正视图为等腰三角形，设C在BD上的射影为E，求出CE，即可得出结论．
解答 解：由题意，三棱锥三视图的正视图为等腰三角形，
△BCD中，BC⊥CD，BC=6，BD=4$\sqrt{3}$，∴CD=2$\sqrt{3}$，
设C在BD上的射影为E，则12=CE$•4\sqrt{3}$，∴CE=$\sqrt{3}$，
故选C．
点评 本题考查三视图，考查学生的计算能力，比较基础．
练习册系列答案
黄冈经典趣味课堂系列答案
启东小题作业本系列答案
相关题目
2．若z是复数，z=$\frac{1-2i}{1+i}$．则z•$\overline{z}$=（ ）
| A． | $\frac{\sqrt{10}}{2}$ | B． | $\frac{\sqrt{5}}{2}$ | C． | 1 | D． | $\frac{5}{2}$ |
3．已知M（-4，0），N（0，-3），P（x，y）的坐标x，y满足$\left\{\begin{array}{l}{x≥0}\\{y≥0}\\{3x+4y≤12}\end{array}\right.$，则△PMN面积的取值范围是（ ）
| A． | [12，24] | B． | [12，25] | C． | [6，12] | D． | [6，$\frac{25}{2}$] |
如图，摄影爱好者在某公园A处发现正前方B处有一根立柱，测得立柱顶端O的仰角和立柱底部B的俯角均为$\frac{π}{6}$，设摄影爱好者的眼睛（S）离地面的高度为$\sqrt{3}$m．
17．若a=logπe，$b={2^{cos\frac{7π}{3}}}$，$c={log_3}sin\frac{17π}{6}$，则（ ）
| A． | b＞a＞c | B． | b＞c＞a | C． | a＞b＞c | D． | c＞a＞b |