题目内容
16.已知实数x,y满足不等式组$\left\{\begin{array}{l}{0≤x≤2}\\{x+y-2≥0}\\{x-y+2≥0}\end{array}\right.$,则目标函数z=3x-4y的最小值m与最大值M的积为-60.分析 作出不等式组对应的平面区域,利用z的几何意义,求出最大值和最小值即可得到结论.
解答 解:不等式组对应的平面区域如图:
由z=3x-4y得y=$\frac{3}{4}$x-$\frac{z}{4}$,
平移直线y=$\frac{3}{4}$x-$\frac{z}{4}$,则由图象可知当直线y=$\frac{3}{4}$x-$\frac{z}{4}$,经过点C时直线y=$\frac{3}{4}$x-$\frac{z}{4}$的截距最大,
此时z最小,当经过点A(2,0)时,直线的截距最小,此时z最大.
由$\left\{\begin{array}{l}{x=2}\\{x-y+2=0}\end{array}\right.$,解得C(2,4),
此时m=z=3×2-4×4=-10,
此时M=3×2=6,
∴Mm=-10×6=-60,
故答案为:-60.
点评 本题主要考查线性规划的应用,根据z的几何意义,利用数形结合是解决本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
12.已知点P(0,3),抛物线C:y2=4x的焦点为F,射线FP与抛物线c相交于点A,与其准线相交于点B,则|AF|:|AB|=( )
| A. | $3:\sqrt{10}$ | B. | $1:\sqrt{10}$ | C. | 1:2 | D. | 1:3 |
9.单位圆中弧长为1的弧所对圆心角的正弧度数是( )
| A. | π | B. | 1 | C. | $\frac{π}{2}$ | D. | 不能确定 |
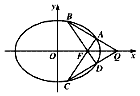 如图,过椭圆M:$\frac{{x}^{2}}{2}$+y2=1的右焦点F作直线交椭圆于A,C两点.
如图,过椭圆M:$\frac{{x}^{2}}{2}$+y2=1的右焦点F作直线交椭圆于A,C两点.