Question

9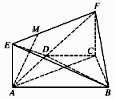．如图，在梯形ABCD中，AB∥CD，AD=CD=CB=a，∠ABC=60°，平面ACFE⊥平面ABCD，四边形ACFE是矩形，AE=a，点M在线段EF上，且MF=2EM．
（1）求证：AM∥平面BDF；
（2）求直线AM与平面BEF所成角的余弦值．

Answer 1

分析 （1）设AC∩BD=N，连接FN，证明：四边形AMFN是平行四边形，AM∥FN，即可证明AM∥平面BDF；
（2）过点C作BF的垂线交BF于点H，求出CH，即可求直线AM与平面BEF所成角的余弦值．

解答 （1）证明：在梯形ABCD中，
∵AB∥CD，AD=CD=CB=a，∠ABC=60°，
∴四边形ABCD是等腰梯形，且∠DCA=∠DAC=30°，∠DCB=120°，
∴∠ACB=90°，∴AC⊥BC，
又∵AC=BD=$\sqrt{3}a$，∴AB=2a．
设AC∩BD=N，连接FN，则CN：NA=1：2，
则AN∥MF且AN=MF，
∴四边形AMFN是平行四边形，∴AM∥FN，
又NF?平面BDF，∴AM∥平面BDF．
（2）解：由题知：AC∥EF，∴点A到平面BEF的距离等于点C到平面BEF的距离，
过点C作BF的垂线交BF于点H，
∵AC⊥CF，AC⊥BC，BC∩CF=C，
∴AC⊥平面BCF，即EF⊥平面BCF，∴CH⊥EF，
又∵CH⊥BF，EF∩BF=F，∴CH⊥平面BEF．
在Rt△BCF中，CH=$\frac{\sqrt{2}}{2}$a，
在△AEM中，AM=$\frac{2\sqrt{3}}{3}$a，
∴直线AM与平面BEF所成角的正弦值为$\frac{CH}{AM}$=$\frac{\sqrt{6}}{4}$，
即直线AM与平面BEF所成角的余弦值为$\frac{\sqrt{10}}{4}$．

点评 本题考查线面位置关系及判定，考查线面角，考查空间想象能力，计算能力，转化能力．