题目内容
已知数列{an}为等比数列,其前n项和为Sn,已知a1+a4=-
,且有S1,S3,S2成等差;
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)已知bn=n(n∈N+),记Tn=|
|+|
|+|
|+…+|
|,求Tn.
| 7 |
| 16 |
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)已知bn=n(n∈N+),记Tn=|
| b1 |
| a1 |
| b2 |
| a2 |
| b3 |
| a3 |
| bn |
| an |
考点:数列的求和,等差数列的性质
专题:等差数列与等比数列
分析:(Ⅰ)设出等比数列的公比q,由S1,S3,S2成等差列式求得q,结合a1+a4=-
求得首项,则数列{an}的通项公式可求;
(Ⅱ)把an、bn代入|
|,整理后利用错位相减法求Tn.
| 7 |
| 16 |
(Ⅱ)把an、bn代入|
| bn |
| an |
解答:
解:(Ⅰ)设等比数列{an}的公比为q,
∵S1,S3,S2成等差,
∴2(a1+a1q+a1q2)=a1+a1+a1q.
整理得:2a1(1+q+q2)=a1(2+q).
∵a1≠0,
∴2+2q+2q2=2+q.
∴2q2+q=0,
又q≠0,∴q=-
.
又a1+a4=a1(1+q3)=-
,
把q=-
代入后可得a1=-
.
∴an=a1qn-1=(-
)×(-
)n-1=(-
)n;
(Ⅱ)∵bn=n,an=(-
)n
∴|
|=|
|=n•2n,
∴Tn=1×21+2×22+3×23+…+n•2n.
2Tn=1×22+2×23+3×24+…+(n-1)•2n+n•2n+1.
∴-Tn=2+22+23+…+2n-n•2n+1=
-n•2n+1.
∴Tn=(n-1)•2n+1+2.
∵S1,S3,S2成等差,
∴2(a1+a1q+a1q2)=a1+a1+a1q.
整理得:2a1(1+q+q2)=a1(2+q).
∵a1≠0,
∴2+2q+2q2=2+q.
∴2q2+q=0,
又q≠0,∴q=-
| 1 |
| 2 |
又a1+a4=a1(1+q3)=-
| 7 |
| 16 |
把q=-
| 1 |
| 2 |
| 1 |
| 2 |
∴an=a1qn-1=(-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
(Ⅱ)∵bn=n,an=(-
| 1 |
| 2 |
∴|
| bn |
| an |
| n | ||
(-
|
∴Tn=1×21+2×22+3×23+…+n•2n.
2Tn=1×22+2×23+3×24+…+(n-1)•2n+n•2n+1.
∴-Tn=2+22+23+…+2n-n•2n+1=
| 2(1-2n) |
| 1-2 |
∴Tn=(n-1)•2n+1+2.
点评:本题考查了等差数列的性质,考查了等比数列的通项公式,训练了错位相减法求数列的和,是中档题.

练习册系列答案
相关题目
曲线f(x)=x3+x-2在点P处的切线的斜率为4,则P点的坐标为( )
| A、(1,0) |
| B、(1,0))或(-1,-4) |
| C、(1,8) |
| D、(1,8)或(-1,-4) |
设函数f(x)=
=x(a∈R)在[-1,1]上有解,则a的取值范围是( )
| 2x+x-a |
| A、[1,2] | ||
B、[-
| ||
| C、[1,3] | ||
D、[-
|
已知A,B,C三点不共线,空间内任一点O满足
=x
+y
+z
(x,y,z∈R),则“x+y+z=1”是“点P在由A,B,C所确定的平面内”的( )
| OP |
| OA |
| OB |
| OC |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
已知△ABC中,b=1,c=
,且
+
+
=
(O是此三角形外心),则
•
=( )
| 2 |
| OA |
| AC |
| OB |
| 0 |
| AB |
| AO |
| A、-2 | B、-1 | C、1 | D、2 |
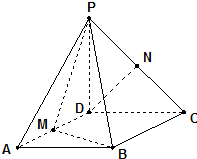 已知四棱锥P-ABCD,底面ABCD是∠A=60°的菱形且PD=AD=2,又PD⊥底面ABCD,点M、N分别是棱AD、PC的中点.
已知四棱锥P-ABCD,底面ABCD是∠A=60°的菱形且PD=AD=2,又PD⊥底面ABCD,点M、N分别是棱AD、PC的中点.