题目内容
已知△ABC中,b=1,c=
,且
+
+
=
(O是此三角形外心),则
•
=( )
| 2 |
| OA |
| AC |
| OB |
| 0 |
| AB |
| AO |
| A、-2 | B、-1 | C、1 | D、2 |
考点:平面向量数量积的运算
专题:计算题,平面向量及应用
分析:由条件可得O为外心,且为BC的中点,则有△ABC为直角三角形,BC为斜边,且BC=
,再由数量积的定义即可得到所求的值.
| 3 |
解答:
解:由于
+
+
=
,
即有
+
=
,
即O为BC的中点,又O是三角形ABC的外心,
则有△ABC为直角三角形,BC为斜边,且BC=
,
则
•
=|
|•|
|•cos∠BAO
=
×
×cos∠ABC
=
×
=1.
故选C.
| OA |
| AC |
| OB |
| 0 |
即有
| OC |
| OB |
| 0 |
即O为BC的中点,又O是三角形ABC的外心,
则有△ABC为直角三角形,BC为斜边,且BC=
| 3 |
则
| AB |
| AO |
| AB |
| AO |
=
| 2 |
| ||
| 2 |
=
| ||
| 2 |
| ||
|
故选C.
点评:本题考查平面向量的数量积及运用,考查三角形的外心的性质,考查运算能力,属于中档题.

练习册系列答案
相关题目
下列现象是随机事件的是( )
| A、天上无云下大雨 |
| B、同性电荷,相互排斥 |
| C、没有水分,种子发芽 |
| D、从分别标有1,2,3,4,5,6,7,8,9,10的10张号签中任取一张,得到1号签 |
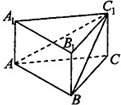 如图,在正三棱柱ABC-A1B1C1中,若AB=2,CC1=1,则点C到平面C1AB的距离等于
如图,在正三棱柱ABC-A1B1C1中,若AB=2,CC1=1,则点C到平面C1AB的距离等于