题目内容
已知复数z满足z•(1-i)=2-i(i为虚数单位),则复数z= .
考点:复数代数形式的乘除运算
专题:数系的扩充和复数
分析:直接利用除法运算法则化简复数为a+bi的形式即可.
解答:
解:z•(1-i)=2-i
z=
=
=
故答案为:
.
z=
| 2-i |
| 1-i |
| (2-i)(1+i) |
| (1-i)(1+i) |
| 3+i |
| 2 |
故答案为:
| 3+i |
| 2 |
点评:本题考查复数的乘除运算,基本知识的考查.

练习册系列答案
相关题目
已知函数f(x)=-ax3+x2-
在(-∞,+∞)上是单调减函数,则实数a的取值范围是( )
| ax |
| 9 |
A、(-∞,-
| ||||
B、[-
| ||||
C、[
| ||||
D、(-∞,
|
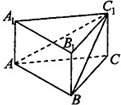 如图,在正三棱柱ABC-A1B1C1中,若AB=2,CC1=1,则点C到平面C1AB的距离等于
如图,在正三棱柱ABC-A1B1C1中,若AB=2,CC1=1,则点C到平面C1AB的距离等于