题目内容
下列一些关于数列{an}的命题:
①若{an}既是等差数列,又是等比数列,则{an}一定是常数数列;
②若{an}是等比数列,则数列{an+an+1}一定也是等比数列;
③若{an}满足递推公式an+1=an•q,则{an}一定是等比数列;
④若{an}的前n项和Sn=qn-1,则{an}一定是等比数列.
其中正确的有 (填写序号)
①若{an}既是等差数列,又是等比数列,则{an}一定是常数数列;
②若{an}是等比数列,则数列{an+an+1}一定也是等比数列;
③若{an}满足递推公式an+1=an•q,则{an}一定是等比数列;
④若{an}的前n项和Sn=qn-1,则{an}一定是等比数列.
其中正确的有
考点:等比关系的确定,等差关系的确定
专题:等差数列与等比数列
分析:①若{an}既是等差数列,设设其公差为d,则2a2=a1+a3,又是等比数列,则a22=a1•a3,可求得d=0,于是知{an}一定是常数数列;
②若{an}是等比数列,不妨令an=(-1)n,则an+1=(-1)n+1,从而可判断则数列{an+an+1}不是等比数列;
③若{an}满足递推公式an+1=an•q,则当q=0时,{an}不是等比数列;
④若{an}的前n项和Sn=qn-1,当q=1时,易知{an}不是等比数列.
②若{an}是等比数列,不妨令an=(-1)n,则an+1=(-1)n+1,从而可判断则数列{an+an+1}不是等比数列;
③若{an}满足递推公式an+1=an•q,则当q=0时,{an}不是等比数列;
④若{an}的前n项和Sn=qn-1,当q=1时,易知{an}不是等比数列.
解答:
解:①若{an}既是等差数列(设其公差为d),又是等比数列,则2a2=a1+a3,a22=a1•a3,
所以,(a1+d)2=a1(a1+2d),解得d=0,故{an}一定是常数数列,①正确;
②若{an}是等比数列,不妨令an=(-1)n,则an+1=(-1)n+1,
所以,an+an+1=0,
所以数列{an+an+1}不是等比数列,即②错误;
③若{an}满足递推公式an+1=an•q,当q=0时,数列{an}不是等比数列,故③错误;
④若{an}的前n项和Sn=qn-1,当q=1时,an=0,显然{an}不是等比数列,故④错误.
综上所述,正确的有①,
故答案为:①.
所以,(a1+d)2=a1(a1+2d),解得d=0,故{an}一定是常数数列,①正确;
②若{an}是等比数列,不妨令an=(-1)n,则an+1=(-1)n+1,
所以,an+an+1=0,
所以数列{an+an+1}不是等比数列,即②错误;
③若{an}满足递推公式an+1=an•q,当q=0时,数列{an}不是等比数列,故③错误;
④若{an}的前n项和Sn=qn-1,当q=1时,an=0,显然{an}不是等比数列,故④错误.
综上所述,正确的有①,
故答案为:①.
点评:本题考查等差关系与等比关系的确定,特别是等边关系的确定,对定义的深刻理解与灵活应用是关键,属于中档题.

练习册系列答案
 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目
已知函数f(x)=|x2-2|,0<m<n,且f(m)=f(n),则m+n的取值范围是( )
| A、(0,2) | ||
B、(2
| ||
C、(
| ||
D、(2,2
|
已知函数f(x)=-ax3+x2-
在(-∞,+∞)上是单调减函数,则实数a的取值范围是( )
| ax |
| 9 |
A、(-∞,-
| ||||
B、[-
| ||||
C、[
| ||||
D、(-∞,
|
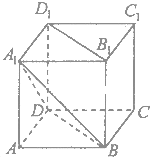 如图,在正方体ABCD-A1B1C1D1中,AB=2.
如图,在正方体ABCD-A1B1C1D1中,AB=2.