题目内容
已知A，B，C三点不共线，空间内任一点O满足
=x
+y
+z
（x，y，z∈R），则“x+y+z=1”是“点P在由A，B，C所确定的平面内”的（ ）
| OP |
| OA |
| OB |
| OC |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
考点：必要条件、充分条件与充要条件的判断
专题：平面向量及应用,简易逻辑
分析：利用所学共面向量基本定理可知A，B，C三点不共线，空间内任一点O满足
=x
+y
+z
（x，y，z∈R），则“x+y+z=1”是“点P在由A，B，C所确定的平面内”的充要条件．必要性由四点共面入手，利用平面向量的加减运算变形证明，充分性直接把x+y+z=1化为x=1-y-z，代入给出的向量表达式加以证明．
| OP |
| OA |
| OB |
| OC |
解答：
解：已知空间任一点O和不共线的三点A，B，C，满足
=x
+y
+z
（x，y，z∈R），
则”x+y+z=1”是“点P位于平面ABC内”的充要条件．
证明如下：
（必要性）由共面向量定理的推论知：四点A、B、C、D共面
?对空间任一点O，存在实数x1、y1，使得
=
+x1
+y1
=
+x1(
-
)+y1(
-
)
=（1-x1-y1）
+x1
+y1
，
取x=1-x1-y1、y=x1、z=y1，
则有
=x
+y
+z
，且x+y+z=1．
（充分性）对于空间任一点O，存在实数x、y、z且x+y+z=1，使得
=x
+y
+z
，
由x=1-y-z得
=（1-y-z）
+y
+z
．
=
+y
+z
，
即：
=y
+z
．
∴四点A、B、C、D共面．
∴空间任意无三点共线的四点A、B、C、D共面的充分必要条件是：
对于空间任一点O，存在实数x、y、z且x+y+z=1，使得
=x
+y
+z
，且x+y+z=1．
∴A，B，C三点不共线，空间内任一点O满足
=x
+y
+z
（x，y，z∈R），则“x+y+z=1”是“点P在由A，B，C所确定的平面内”的充要条件．
故选：C．
| OP |
| OA |
| OB |
| OC |
则”x+y+z=1”是“点P位于平面ABC内”的充要条件．
证明如下：
（必要性）由共面向量定理的推论知：四点A、B、C、D共面
?对空间任一点O，存在实数x1、y1，使得
| OA |
| OB |
| BC |
| BD |
| OB |
| OC |
| OB |
| OD |
| OB |
=（1-x1-y1）
| OB |
| OC |
| OD |
取x=1-x1-y1、y=x1、z=y1，
则有
| OA |
| OB |
| OC |
| OD |
（充分性）对于空间任一点O，存在实数x、y、z且x+y+z=1，使得
| OA |
| OB |
| OC |
| OD |
由x=1-y-z得
| OA |
| OB |
| OC |
| OD |
| OA |
| OB |
| BC |
| BD |
即：
| BA |
| BC |
| BD |
∴四点A、B、C、D共面．
∴空间任意无三点共线的四点A、B、C、D共面的充分必要条件是：
对于空间任一点O，存在实数x、y、z且x+y+z=1，使得
| OA |
| OB |
| OC |
| OD |
∴A，B，C三点不共线，空间内任一点O满足
| OP |
| OA |
| OB |
| OC |
故选：C．
点评：本题考查了充要条件问题，考查了共面向量基本定理的推广应用，是中档题．
练习册系列答案
相关题目
已知函数f（x）=
（k∈R）．若函数y=|f（x）|+k有三个零点，则实数k的取值范围是（ ）
|
| A、k≤-2 |
| B、-2≤k＜-1 |
| C、-1＜k＜0 |
| D、k≤2 |
已知复数z=1+ai（a∈R）（i是虚数单位）在复平面上表示的点在第四象限，且|z|=
，则a=（ ）
| 5 |
| A、2 | ||
| B、-2 | ||
C、
| ||
D、-
|
已知函数f（x）=-ax3+x2-
在（-∞，+∞）上是单调减函数，则实数a的取值范围是（ ）
| ax |
| 9 |
A、（-∞，-
| ||||
B、[-
| ||||
C、[
| ||||
D、（-∞，
|
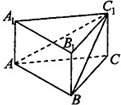如图，在正三棱柱ABC-A1B1C1中，若AB=2，CC1=1，则点C到平面C1AB的距离等于