题目内容
5.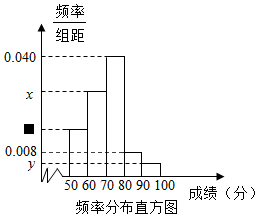 某中学为了解某次竞赛成绩情况,从中抽取了部分学生的分数(得分取正整数,满分为100分)作为样本进行统计,请根据下面尚未完成并有局部污损的频率分布表和频率分布直方图解决下列问题:
某中学为了解某次竞赛成绩情况,从中抽取了部分学生的分数(得分取正整数,满分为100分)作为样本进行统计,请根据下面尚未完成并有局部污损的频率分布表和频率分布直方图解决下列问题:频率分布表:
| 组别 | 分组 | 频数 | 频率 |
| 第1组 | [50,60) | 9 | 0.18 |
| 第2组 | [60,70) | a | ▓ |
| 第3组 | [70,80) | 20 | 0.40 |
| 第4组 | [80,90) | ▓ | 0.08 |
| 第5组 | [90,100] | 2 | b |
| 合计 | ▓ | ▓ |
(2)在选取的样本中,从竞赛成绩是80分以上(含80分)的同学中随机抽取2名同学参加座谈,求所抽取的2名同学来自同一组的概率.
分析 (1)由题意知,t先求出样本总数,由此能求出a,b,x,y的值.
(2)由题意知第4组竞赛成绩是80分以上(含80分)的同学有4人,第5组竞赛成绩是80分以上(含80分)的同学有2人,共6人,由此利用等可能事件概率计算公式能求出所抽取的2名同学来自同一组的概率.
解答 解:(1)由题意知,样本总数n=$\frac{9}{0.18}$=50,b=$\frac{2}{50}$=0.04,
y=$\frac{0.04}{10}=0.004$,x=$\frac{1-0.18-0.4-0.08-0.04}{10}$=0.03,
a=(1-0.18-0.4-0.08-0.04)×50=15.
(2)由题意知第4组竞赛成绩是80分以上(含80分)的同学有4人,
第5组竞赛成绩是80分以上(含80分)的同学有2人,共6人,
从竞赛成绩是80分以上(含80分)的同学中随机抽取2名同学参加座谈,
基本事件总数n=${C}_{6}^{2}$=15,
所抽取的2名同学来自同一组包含的基本事件个数m=${C}_{4}^{2}+{C}_{2}^{2}$=7,
∴所抽取的2名同学来自同一组的概率p=$\frac{7}{15}$.
点评 本题考查概率的求法,是中档题,解题时要认真审题,注意频率分布直方图和频率分布表的性质的合理运用.

练习册系列答案
相关题目
20.复数$\frac{-i}{1-2i}(i$是虚数单位)的共轭复数为( )
| A. | $-\frac{2}{5}+\frac{i}{5}$ | B. | $-\frac{2}{5}-\frac{i}{5}$ | C. | $\frac{2}{5}-\frac{i}{5}$ | D. | $\frac{2}{5}+\frac{i}{5}$ |
10.设α为第二象限,若sinα+cosα=-$\frac{\sqrt{10}}{5}$,则tan(α+$\frac{π}{4}$)等于( )
| A. | 2 | B. | $\frac{1}{2}$ | C. | -$\frac{1}{2}$ | D. | -2 |

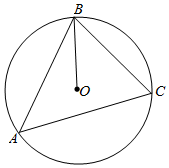 如图所示,圆O是△ABC的外接圆,BA=m,BC=$\frac{4}{m}$,∠ABC=60°,若$\overrightarrow{BO}=x\overrightarrow{BA}$+y$\overrightarrow{BC}$,则x+y的最大值是$\frac{2}{3}$.
如图所示,圆O是△ABC的外接圆,BA=m,BC=$\frac{4}{m}$,∠ABC=60°,若$\overrightarrow{BO}=x\overrightarrow{BA}$+y$\overrightarrow{BC}$,则x+y的最大值是$\frac{2}{3}$.