题目内容
13.设θ为第二象限角,若$tan(θ+\frac{π}{3})=\frac{1}{2}$,则sinθ+$\sqrt{3}$cosθ=-$\frac{2\sqrt{5}}{5}$.分析 由条件利用同角三角函数的基本关系求得sin(θ+$\frac{π}{3}$)的值,再利用两角差的正弦公式求得要求式子的值.
解答 解:∵θ为第二象限角,若$tan(θ+\frac{π}{3})=\frac{1}{2}$>0,∴θ+$\frac{π}{3}$为第三象限角,
由$\frac{sin(θ+\frac{π}{3})}{cos(θ+\frac{π}{3})}$=$\frac{1}{2}$,sin(θ+$\frac{π}{3}$)<0,cos(θ+$\frac{π}{3}$)<0,${sin}^{2}(θ+\frac{π}{3})$+${cos}^{2}(θ+\frac{π}{3})$=1,
求得sin(θ+$\frac{π}{3}$)=-$\frac{\sqrt{5}}{5}$,
则sinθ+$\sqrt{3}$cosθ=2sin(θ+$\frac{π}{3}$)=-$\frac{2\sqrt{5}}{5}$,
故答案为:-$\frac{2\sqrt{5}}{5}$.
点评 本题主要考查同角三角函数的基本关系,两角差的正弦公式的应用,属于基础题.

练习册系列答案
相关题目
4.已知F1,F2分别是双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左右两个焦点,若在双曲线C上存在点P使∠F1PF2=90°,且满足2∠PF1F2=∠PF2F1,那么双曲线C的离心率为( )
| A. | $\sqrt{3}$+1 | B. | 2 | C. | $\sqrt{3}$ | D. | $\frac{\sqrt{5}}{2}$ |
8.已知函数f(x)=(x2+ax+b)ex,当b<1时,函数f(x)在(-∞,-2),(1,+∞)上均为增函数,则$\frac{a+b}{a-2}$的取值范围是( )
| A. | (-2,$\frac{2}{3}$] | B. | [-$\frac{1}{3}$,2) | C. | (-∞,$\frac{2}{3}$] | D. | [-$\frac{2}{3}$,2] |
18.运行如图所示的程序框图,则输出的结果是( )
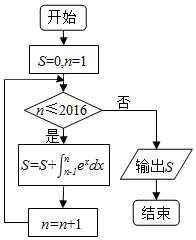

| A. | e2016-e2015 | B. | e2017-e2016 | C. | e2015-1 | D. | e2016-1 |
5.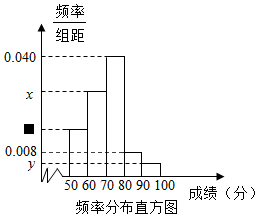 某中学为了解某次竞赛成绩情况,从中抽取了部分学生的分数(得分取正整数,满分为100分)作为样本进行统计,请根据下面尚未完成并有局部污损的频率分布表和频率分布直方图解决下列问题:
某中学为了解某次竞赛成绩情况,从中抽取了部分学生的分数(得分取正整数,满分为100分)作为样本进行统计,请根据下面尚未完成并有局部污损的频率分布表和频率分布直方图解决下列问题:
频率分布表:
(1)写出a,b,x,y的值;
(2)在选取的样本中,从竞赛成绩是80分以上(含80分)的同学中随机抽取2名同学参加座谈,求所抽取的2名同学来自同一组的概率.
 某中学为了解某次竞赛成绩情况,从中抽取了部分学生的分数(得分取正整数,满分为100分)作为样本进行统计,请根据下面尚未完成并有局部污损的频率分布表和频率分布直方图解决下列问题:
某中学为了解某次竞赛成绩情况,从中抽取了部分学生的分数(得分取正整数,满分为100分)作为样本进行统计,请根据下面尚未完成并有局部污损的频率分布表和频率分布直方图解决下列问题:频率分布表:
| 组别 | 分组 | 频数 | 频率 |
| 第1组 | [50,60) | 9 | 0.18 |
| 第2组 | [60,70) | a | ▓ |
| 第3组 | [70,80) | 20 | 0.40 |
| 第4组 | [80,90) | ▓ | 0.08 |
| 第5组 | [90,100] | 2 | b |
| 合计 | ▓ | ▓ |
(2)在选取的样本中,从竞赛成绩是80分以上(含80分)的同学中随机抽取2名同学参加座谈,求所抽取的2名同学来自同一组的概率.
